アメリカン デス トライアングルを初等力学で考える(同一スリング長での比較)
前回の記事でアメリカンデストライアングル(以下、ADT)において上2つのボルトにかかる力を初等力学で求めました。
しかしfacebookやtwitterで突っ込まれたのですが、実はこの議論は現場に適用するには厳密には正しくなかったのです。
なぜかというと、実際は一定の長さのスリングでADTにするか流動分散や固定分散で安全な支点を構築するかを選択することになります。
するとスリングが成す角度θはこの2つの場合で異なるのです。
なので同じθ=60°などでADTの場合と安全な支点の場合で比べることはそもそも実際の場合に即してはいなくて、同じスリング長の場合にどうなるかという前提での比較が必要だったのです。
そしてこの前提において一応紙にざっと計算を書いて求めました。
ですがそれを丁寧にテキストベースで議論するのは大変なので、僕の計算した紙の写真を貼り付けてざっと説明します!笑
どんな場合でもADTは選択すべきでないことの証明
まず写真を貼りますね。
途中かなりテクニカルな三角関数の変換などもしていますが、紙面の都合上説明を省いている箇所も多いです。
本当に興味がある方だけ計算を追ってみてください。
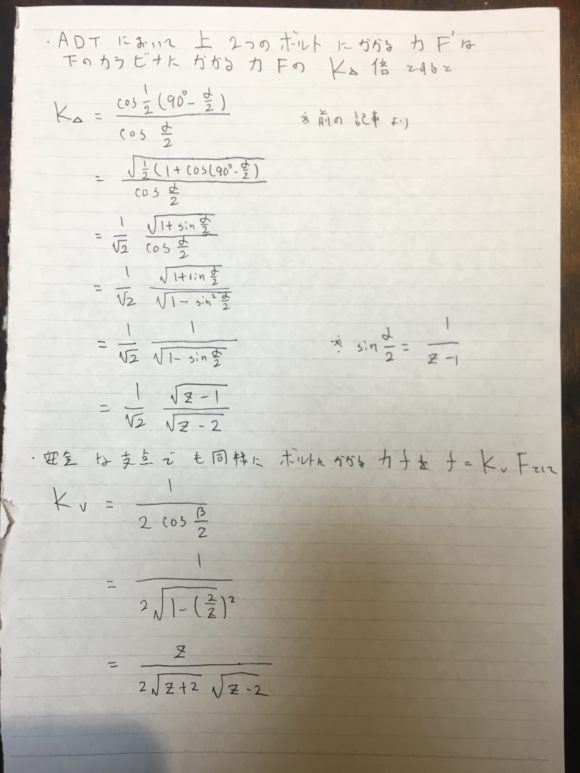
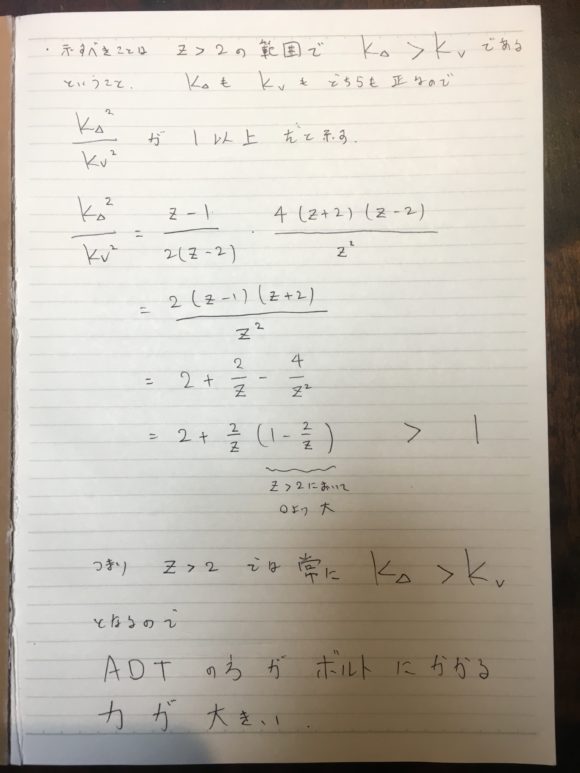
えー何をしているかを説明すると、
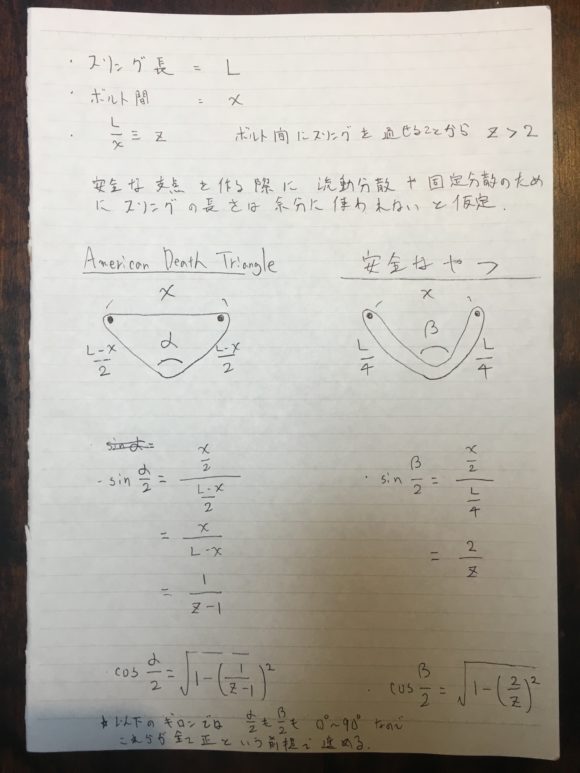
ボルト間隔:x
スリング長:L
として、この比率z=L/xとしています。
スリングをボルト間に通せるギリギリのときz=2なので、zは2より常に大きいという前提を置きます。
(ボルトの間隔が30cmだった場合60cmスリングはADTを選択しても三角形にならないですよね。)
そしてADTの場合に、スリングが成す角度をα、ボルトにかかる力は支点にかかる力FのKΔ倍
安全な支点の場合に、スリングが成す角度をβ、ボルトにかかる力は支点にかかる力FのKv倍
として、2より大きい全てのzにおいて、KΔ>Kvとなることを示したのです。
ただし、安全な支点を構築する時に流動分散なり固定分散をするためにスリングの長さは短くならないという仮定を置いています。
ここは現実世界とは異なるのですが、この仮定を置かないと例えば固定分散を作るためにスリングを目一杯までオーバーハンドノットしてβ=180°などとしてしまえば、流石にADTよりもボルトにかかる力は大きくなってしまうからです。
なので、一応結論としては(流動分散や固定分散を作る際にスリングをかなり余計に使わなければ)ADTはどんなときでも選択すべきでない。
ということになります。
グラフで見てみる
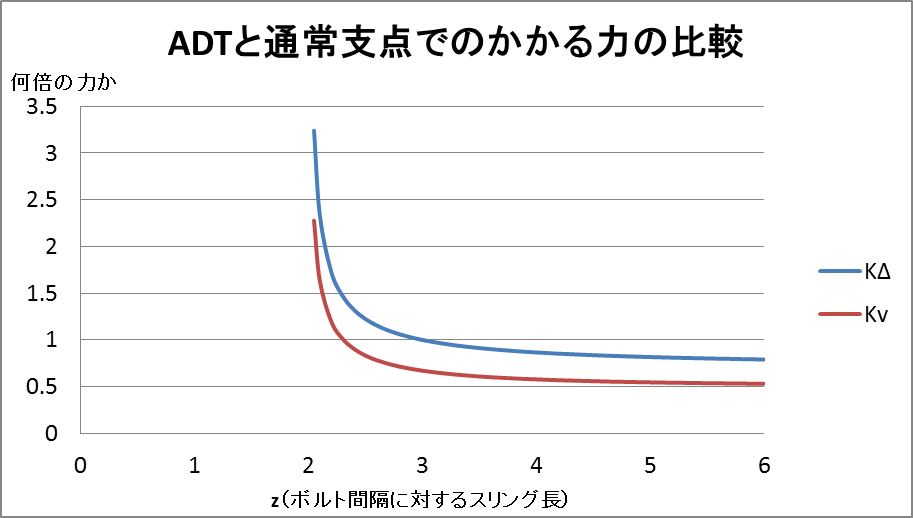
KΔとKvをzの関数としてグラフで表したものが以下です。
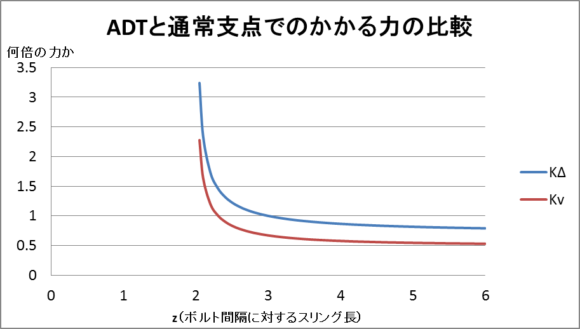
常にKΔがKvを上回っている、すなわちADTの方がボルトにかかる力が大きいことがわかります。
z=2でどちらも無限大に発散していきそうなのは、スリングが成す角度が180°に近づくとボルトに非常に大きな力がかかってしまうということです。
z=3のとき、ADTではスリングが正三角形をなすのでちゃんとKΔ=1となっていますね。
そしてzが大きくなる、つまりスリングが成す角度が0°に近づくと、安全な支点ではボルトにかかる力が半分になるのですがKvはきちんと0.5に近づいています。
ADTの場合はスリングが成す角度が0°に近づいてもボルトは下方向と横方向の2方向にスリングから力を受けるため、その合力は1/√2≒0.71までしか軽減されないこともグラフから読み取れます。
正直直感的にわかることだったのですが何か気持ち悪かったので久々に計算してみました。
あー楽しかった!
ではまた!
-
前の記事
アメリカン デス トライアングルを初等力学で考える 2018.06.27
-
次の記事

2018年リードワールドカップ開幕!第1戦出場選手とその戦績 2018.07.04
