アメリカン デス トライアングルを初等力学で考える

今日はクライミングの中でも少しマニアックな話。

マルチピッチクライミングなどでの作法をきちんと力学的に自分の頭で整理しておきたいなと思っておりまして、今回は非常に簡単ですがその第一弾。

アメリカン デス トライアングルを初等力学（というか高校物理の初歩）を使って考えてみました。

アメリカンデストライアングルとは

声に出したいクライミング用語の筆頭に「アメリカン デス トライアングル」(American Death Triangle)というものがあります。

これはマルチピッチクライミングなどでの間違った支点構築（終了点やビレイ点になりえる安全なポイントの構築）の1つで以下の写真の様な状態を指します。

実際のものからは簡略化していますが、上2つのカラビナがボルト等で岩と固定されていて、そこにスリングを通すことで下に垂れ下がっているカラビナを支点としていると見てください。

本来であればこの下のカラビナにロープを通して終了点としたり、同じ場所にセルフビレイを取ったりするために使いたいのです。

これの何がまずいのかというと、下の支点となっているカラビナに力がかかった場合に上2つのカラビナには必要以上に（スリングから下方向だけでなく横方向にも）力がかかってしまい、場合によってはボルトが抜けるなどして支点が崩れる可能性が高いと言われています。

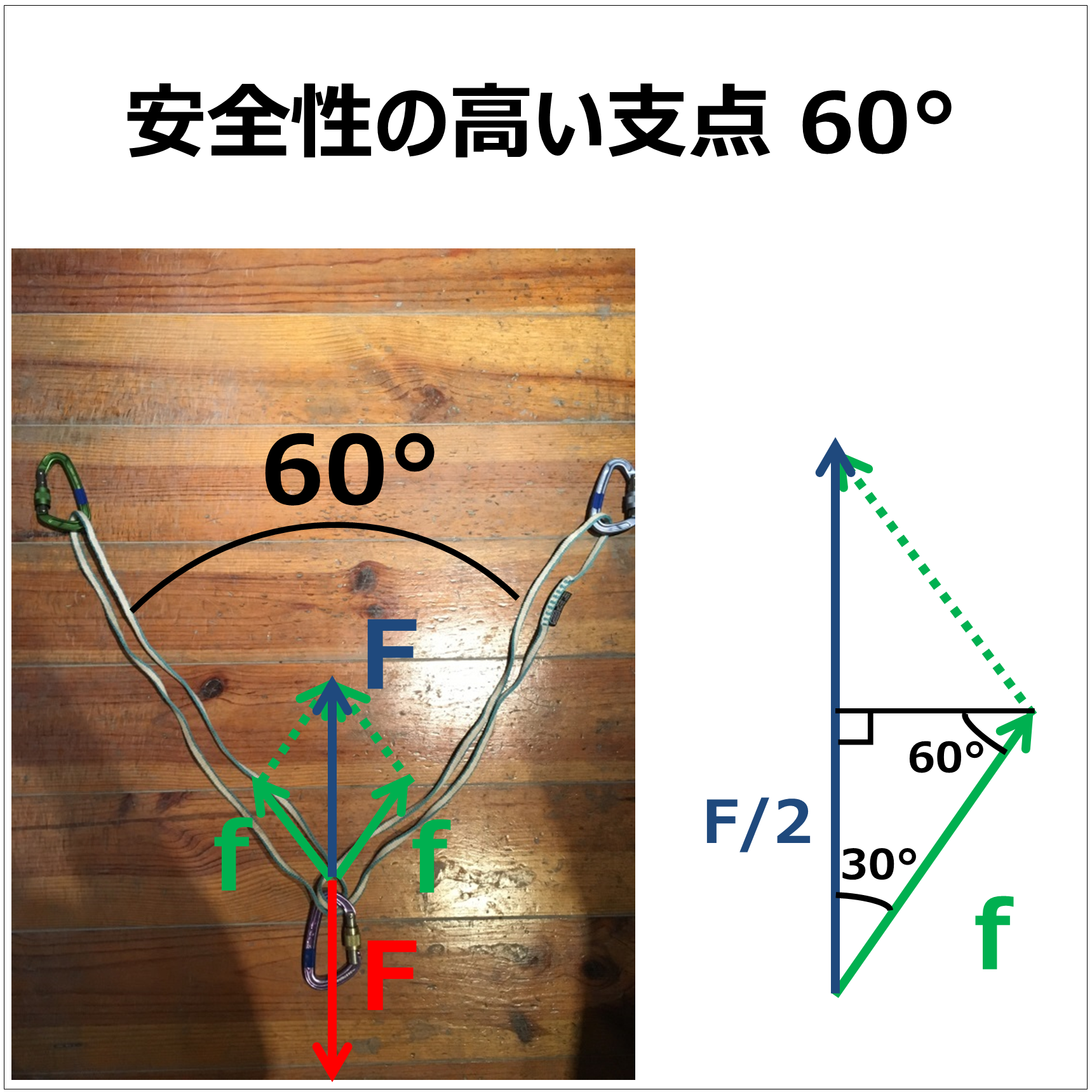
安全性の高い支点とは

高い安全性できちんと構築された支点と比べてみましょう。

（スリングの通し方は流動分散としていますが、固定か流動かなどは今回の話とは関係ないので一旦触れずにおきます）

先ほどとは違い、上2つのカラビナの間にはスリングが通っていなく下の支点となっているカラビナとのみ繋がっています。

このような場合は下の支点となっているカラビナに力がかかっても、上の2つのカラビナは下方向にのみ引かれるのでアメリカン デス トライアングルとは違い余計な横方向の力がかかりません。

ですので上の2つのカラビナが連結されているボルトなどが抜ける可能性はアメリカン デス トライアングルよりは低いのです。

力学的に考える

アメリカン デス トライアングルを避けるべき話は直感的に理解できるので、おそらく上記のような説明でも十分かもしれません。

一応僕が調べた限りは日本語の本やウェブページだと「角度がxx度の時は、○○くらいの力がかかる」といったことは載っていても計算理由までは見当たりませんでした。

ですので今回は簡単な物理を使って力学的に理解をしてみたいと思います。

安全性の高い支点

まず支点となっているカラビナにロープ等を通して下方向にかかる力の大きさをFとします。（図の赤）

カラビナにかかる力はつりあっているので、スリングからも上方向にFの力で引かれていることになります。（図の青）

スリングは実際には右上方向と左上方向の2つの張力で引いているはずであり、張力はスリングのどこでも一定と考えて良いため共に大きさfと置きます。（図の緑）

とするとこの2つのfの合力がFになっているわけです。

そして上の2つのカラビナもfの力でスリングから引かれているのでこのfを求めれば良いです。

スリングが成す角度が60°の場合を考えてみると、Fとfが成す三角形は図の右側に拡大したように「90°、60°、30°」の直角三角形であり、その辺の長さは斜辺がf、もう一辺の長い方がF/2となります。

この直角三角形の辺比は1:2:√3となっているので、

f：F/2=2：√3

より

f=F/√3

が導け、fはおよそFの0.58倍の大きさの力であることがわかりました。

これは本などでよく説明されている数字と一致します。

つまり上の2つのカラビナには下の支点にかかる力が半分近く軽減されてかかることになるのです。

そして直感的にも理解できますが、このスリングが成す角度が小さくなるほど力は軽減されます。

0°の場合を考えるともはや説明がほぼ必要ないですが、上方向にかかる2つのfの和がFなので

f=F/2となり、1/2にまで軽減していることがわかります。

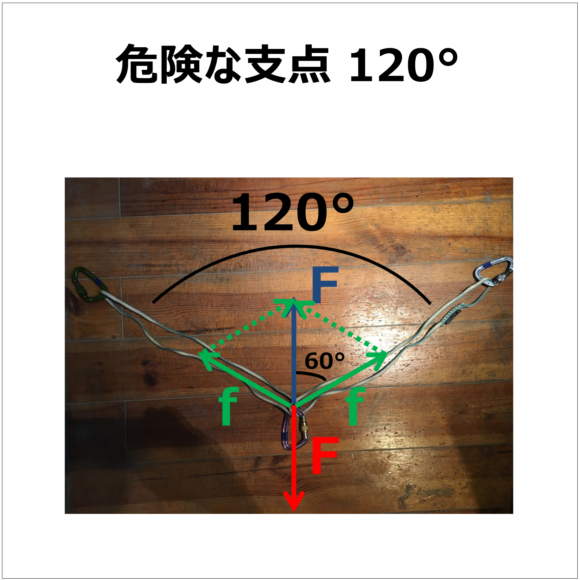
一方でもしこの角度が120°であった場合はこちらも図を見ると一目瞭然なのですが、fとFが成す三角形が正三角形となるので

f=Fとなってしまい、力は全く軽減されずそのまま上の2つのカラビナにもかかることとなってしまいます。

ですので一般的には60°以下程度にとどめておいた方が良いなどと言われています。

一応興味がある方のためにスリングが成す角度が一般角θの場合でも書いておきます。

60°の場合と同様の三角形を考えればθ/2を含む直角三角形が取り出せるので

cos(θ/2)=(F/2)/f、という関係が得られ

f=F/[2cos(θ/2)]

が導かれます。

なのでθが150°などになると、f=1.93Fとなってかなり危険な状態になることがわかります。

アメリカン デス トライアングル

ではいよいよ本題でアメリカン デス トライアングルの場合を考えてみましょう。

上で考えた条件と同じにするため、スリングがなす角度を60°にしてみます。

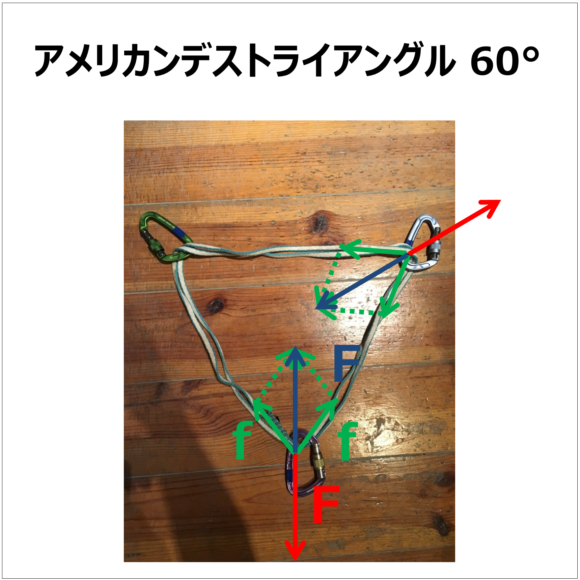
同様にスリングの張力はfなのですが、先ほどと違うのは上の2のカラビナの間にもスリングが通っているためどちらにも2つのfの合力がかかるという点です。

そしてスリングの内角は60°であり正三角形なので対称性から上の2つのカラビナにスリングからかかる2つのfの合力の大きさもFとなるとわかります。

つまり上のカラビナにかかる力は全く軽減されずFがそのままかかるのです。

同じ60°のときに安全な支点では0.58倍にまで軽減されていたことと比べると大きな違いですね。

こちらも一般角θの時を簡単に説明しておきますね。（図などは省略するので興味がある人は描いてみてください）

スリングがなす三角形は「θ、90°-θ/2、90°-θ/2」の二等辺三角形です。

上のカラビナにかかる2つのfの合力の大きさをF’とすると、一番初めの安全な支点での例と同じことを考えてあげれば、θのところを（90°-θ/2)に置き換えればよいので

cos[(90°-θ/2)/2]=(F’/2)/f、という関係が得られます。

よって、F’=2f cos(45°-θ/4)

ここにf=F/[2cos(θ/2)]を代入すると

F’=F cos(45°-θ/4)/cos(θ/2)

が得られます。（もっときれいになりそうだけど、、、）

ここにいくつか角度をあてはめると

θ=120°だとF’=1.93F

θ=150°だとF’=3.83F

などとなり、数倍もの力が上2つのカラビナにはかかってしまうことがわかります。

つまりアメリカン デス トライアングルを作ってしまうこと自体危険なのですが、スリングが成す角度がより大きい状態で作ってしまうとその危険度も跳ね上がるのです。

終わりに

簡単にサラッとやるつもりが、なぜか結構量が多くなって完全に自己満になってしまいました、、、。

まぁでもここまでの議論をひっくり返すようですが、直感的に「あ、アメリカン デス トライアングルは横にも引かれるからやばそう」とわかることが一番大事だと思います。笑

しかし自分の中ではこの計算で多角的に大分理解が進んだので良しとします。

この他にも力学的に理解したいことがいくつかあるので需要があるかはわかりませんがこのシリーズはいつかまたやるかもしれません。

ではでは。

！追記！

同一スリング長という仮定で比べないと正しい議論ではないという突っ込みを受けたので、追加記事を書きました。

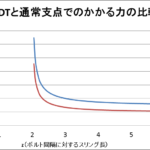
アメリカン デス トライアングルを初等力学で考える（同一スリング長での比較）