カムはなぜ決まるのかを初等力学で考える 後編
- 2018.08.31
- データ&ルール 上達方法 岩場の記録 科学するクライミング

カムはなぜ決まるのかの後編です。
前編ではカムの力学的作用について考えたので、後編ではカムの歯の数学的特徴について少し詳しく見ていきます。
<前編>
カムの歯の特徴のおさらい
前編でも何度も述べましたが大切なことなので何度も書いておくと、
カムは平行なクラックに決める場合、歯の回転角度によらず「クラック」と「クラックとの接点へ軸中心から引いた直線」との角度が常に一定となるように作られています。
つまり下の図で言えば、
赤い線:クラック
黒い線:水平線
緑の線:クラックとの接点へ軸中心から引いた直線
として、
クラック(赤)とクラックとの接点へ軸中心から引いた直線(緑)が成す角度αは常に一定であり、
もちろん水平線(黒)とクラックとの接点へ軸中心から引いた直線(緑)が成す角度βも常に一定である、ということです。
このβはカムアングルと呼ばれ、例えばキャメロットでは14°程度に設計されています。

歯は対数螺旋
一体どうやってカムの歯はこんな摩訶不思議で素敵で便利な特徴を持つことができるのでしょうか。
その秘密は歯が対数螺旋という形状になっていることに由来します。
対数螺旋は詳しくはWikipedia先生などを見て欲しいのですが、数式で記述すると
rを原点からの距離
eは自然対数の底
θをx軸からの角度
A,bを実数値(Aは正、αと紛らわしいのでaではなく大文字のAとします)
として
極座標系で
$$\bf r=Ae^{bθ}$$
x,yの直交座標系の媒介変数表示で
$$\bf x=rcosθ=Ae^{bθ}cosθ$$
$$\bf y=rsinθ=Ae^{bθ}sinθ$$
と表される曲線のことです。
つまりx軸とAの位置で交わるところから、角度θが増えるにつれて原点からの距離もe^(bθ)だけどんどんと増えていくような曲線です。
実際に見た方が理解し易いと思うので試しに適当にA=0.04、b=0.5で対数螺旋を書いてみると以下の様になります。
(Function viewというソフトを使用)
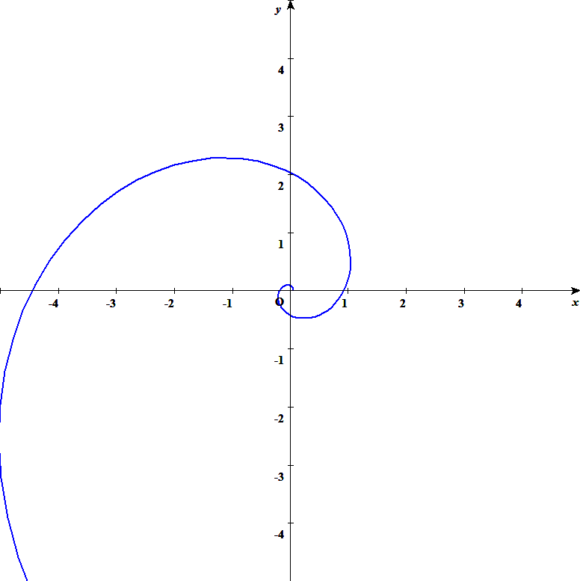
bが負だと逆回りになり、b=0だとr=Aの円となります。
確かになんとなくカムの歯の形状っぽいですよね。
自然界だと貝殻の形や鳥が獲物を狙う時の軌跡などに現れるようです。
『Steel Ball Run』に出てくる黄金の回転もこの対数螺旋のことなので、ジョジョフリークならば当然知っていますよね!

対数螺旋だとカムアングルが常に一定となる証明
少し話が逸れましたが、本題に戻ります。
今調べたいのはカムの歯を対数螺旋となるように作ったとしたらカムアングルβや(90°-β)であるα、すなわち「原点を通る直線」と「その直線と曲線の接点での接線」が成す角度、が一定となるということです。
<原点を通る直線(緑)と接線(赤)が成す角度一定となる>
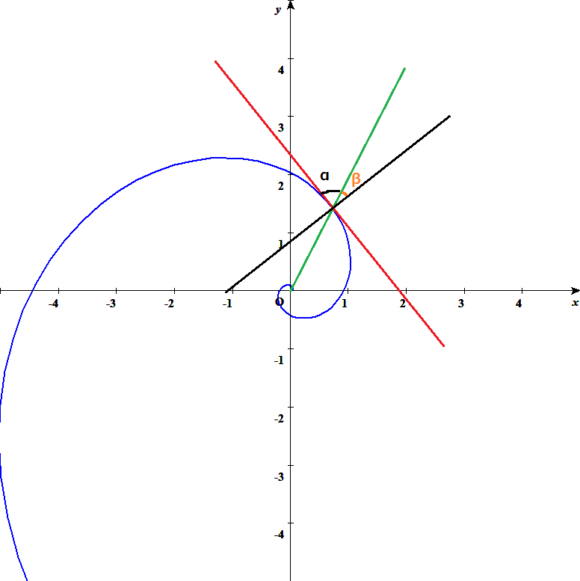
黒い線はカムに見立てるならば水平線となります。
原点を通る直線(緑)の方向ベクトルは(cosθ,sinθ)。
接線(赤)の方向ベクトルは角度dθだけ動いた時にどれだけ接点が変化するかを考えれば良いので、
$$\left( \frac{dx}{dθ},\frac{dy}{dθ} \right)$$
を計算します。
$$\frac {dx}{dθ}$$
$$=\frac{d(Ae^{bθ}cosθ)}{dθ}$$
$$=Abe^{bθ}cosθ-Ae^{bθ}sinθ$$
$$=Ae^{bθ}(bcosθ-sinθ)$$
$$=r(bcosθ-sinθ)$$
$$\frac {dy}{dθ}$$
$$=\frac{d(Ae^{bθ}sinθ)}{dθ}$$
$$=Abe^{bθ}sinθ+Ae^{bθ}cosθ$$
$$=Ae^{bθ}(bsinθ+cosθ)$$
$$=r(bsinθ+cosθ)$$
角度αを求めるには緑の方向ベクトル
$$(cosθ,sinθ)$$
と赤の方向ベクトル
$$\left( \frac{dx}{dθ},\frac{dy}{dθ} \right)$$
の内積を二つのベクトルの大きさの絶対値の積で割ることでcosαを出してやれば良いです。
二つのベクトルの内積
$$=r(bcosθ-sinθ)cosθ+r(bsinθ+cosθ)sinθ$$
$$=rbcos^{2}θ+rbsin^{2}θ$$
$$=rb$$
緑の方向ベクトルの絶対値は1
赤の方向ベクトルの絶対値
$$=r\sqrt{b^{2}cos^{2}θ-2bcosθsinθ+sin^{2}θ+b^{2}sin^{2}θ+2bcosθsinθ+cos^{2}θ}$$
$$=r\sqrt{b^{2}+1}$$
よって
$$\bf cosα$$
$$=\frac{rb}{1・r\sqrt{b^{2}+1}}$$
$$\bf =\frac{b}{\sqrt{b^{2}+1}}$$
というrにもθにもよらない一定値を得ます。
つまりαは対数螺旋の曲線上ならばどこでも常に一定。
すなわちカムの歯が対数螺旋で設計されていればカムアングルは歯がどれだけ回転していようと常に一定だと言えるわけです。
めでたしめでたし。
ここでした計算なども含めて例えば「科学の言語としての数学」というスライドなどに詳しく載っているので興味がある方は是非読んでみてください。
実際のカムで検証
一応カムが本当に対数螺旋となっているのか検証してみましょう。
キャメロットでは
$$r=Ae^{bθ}$$
のAとbがどのような値になるかを考えたいのですが、まずAは実はどのような値でも構いません。
なぜなら対数螺旋は自己相似となっているので、Aが変化しても曲線が定数倍されるだけで対数螺旋が回転されて拡大縮小されるだけなのです。
つまりAはいくつであっても適切なbを選んでやれば、その対数螺旋の中のどこかにカムの歯の形が出現するはずです。
bを決めるにあたってキャメロットではα=76°(β=14°)となることから対数螺旋の形を決定できます。
$$cosα=\frac{b}{\sqrt{b^{2}+1}}$$
なので
を両辺二乗して
$$cos^{2}α=\frac{b^{2}}{b^{2}+1}$$
より
$$b^{2}$$
$$=\frac{cos^{2}α}{1-con^{2}α}$$
$$=\frac{1}{tan^{2}α}$$
となり、α=76°ならばtanαは正なので
$$b$$
$$=\frac{1}{tanα} α=90°-βなので$$
$$=tanβ$$
$$=tan14°$$
$$≒0.25$$
を得ます。
(対数螺旋の式のeの指数に乗る定数bがtanを使ってこのようにシンプルに表すことができるというのはClimbing Cam Geometryで幾何的にも解説しています。
前編において滑らない条件として静止摩擦係数よりもtanβが小さいことが導かれたので、曲線の形を決定づけているtanβがeの指数に登場することは納得できます。参考文献を読み切っていないので厳密にその意味合いを理解し切ってはいないですが)
つまりAを適当に2とおいてbにtan14°を入れると
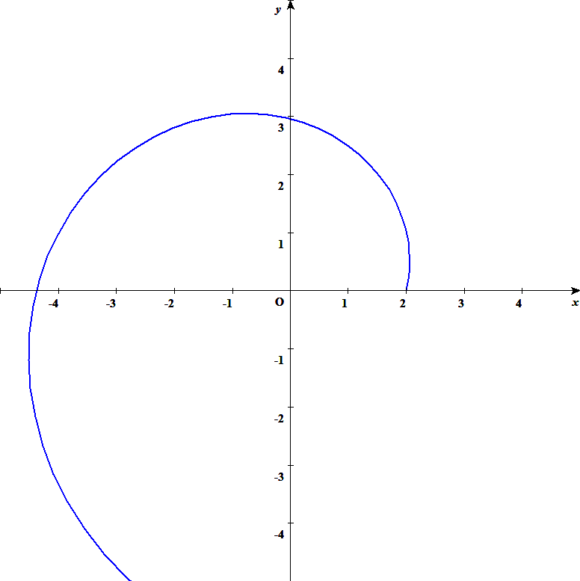
こんな対数螺旋の曲線になります。
これめちゃくちゃカムっぽいですね!
実際にキャメロットC4の6番を重ねてみると、、、

ぴったり手前の緑の歯の形に青い対数螺旋曲線が一致しました!
(スケールと原点を合わせるために、A=1.9、中心(0.7,-0.45)としている)
いや当たり前なのですが気持ち良いですね。
そして一応検証しておくと対数螺旋はbの値さえ同じならば自己相似となっているはずです。
eの肩に乗っているθが例えば一定角度φだけ足されてもe^φが前に出て来て全体がe^φ倍されるだけなので。
ですのでカムアングルが同じならばどのカムの自己相似なわけです。
キャメロットならばカムアングルβは14°程度で一定なはずなので、C4の6番だけでなく、例えば0.3番などで試しても、、、

このように見事に対数螺旋曲線と一致しました!
(スケールと原点を合わせるために、A=0.55、中心(0.9,0.6)としている)
つまり僕らが扱っているカムは同じメーカーの同じシリーズならば(カムアングルはおそらく一定なので)それぞれ拡大縮小したものだったのですね。
終わりに
かなり趣味に突っ走りましたが、いかがでしたでしょうか。
それにしても数学や物理って面白くて美しいですね。
勉学や大学の研究という道を離れて他の分野へ進みましたが、そのことでむしろ数学や物理をある程度自分の道具として使えることが如何に人生の大きな財産となっているかをあらためて実感させられます。
クライミングに限らず前職のコンサルなどでもきっと役に立っていたはず。
※※
以下2018年9月8日に改善
でも書いてて思ったのがテキストで数式を打つのがメンドウ&読みづらすぎますね。
なんかしらの数式プラグインとかを入れないと。
これとか試してみようかな。
※※
最後になりますが、対数螺旋をカムに応用するという素晴らしいことを思いついたのはロウアルパインの共同設立者であるロウ・グレッグのようですね。
その後レイ・ジャーディンが現在の形に応用してワイルドカントリーのフレンズという製品になったのかな。
このあたりの歴史は詳しくないけれど
や
に載っているようです。
また、ちょくちょくこの「科学するクライミング」や「初等力学」シリーズも書いていくのでお楽しみに!
どれだけ需要があるかわかりませんが自分が好きなことを書くのが一番なのでね。
ではでは。
-
前の記事

カムはなぜ決まるのかを初等力学で考える 前編 2018.08.29
-
次の記事

クライミング世界選手権の歴代優勝者と2018注目選手 2018.09.05
