“Withコロナ”の時代に僕らはクライミングとどう向き合うか 前編:収束シナリオを考える
新型コロナウイルスの影響で、大都市圏は緊急事態宣言が出され、多くの商業クライミングジムは休業を余儀なくされ、公式コンペも中止や延期、そして岩場で登ることも自粛ムードとなっています。
僕は元々インドア少年だったので家で過ごすことに苦はなく、フィンガーボード等での地味トレも楽しいし、久々に妻と2人でゆっくり過ごすことも悪くはないです。
ただクライミングでやりたいこと、行ってみたい場所、成し遂げたいことはまだまだ盛りだくさんですし、一生このまま家でトレーニングして死ぬわけにもいかないというのがもちろん本音。
少なくとも、新型コロナウイルスの蔓延状況とそれに伴う社会状況がどうなっていきそうなのかの見通しは持ちたいです。
ということで、今回は僕の収集した情報を元に自分の頭で考えることができる範囲で、
・新型コロナウイルスの流行はどうなるのか
・収束するのはいつなのか。そもそも収束ってなんなのか
・クライミング業界はこの先どうなっていくのか
・僕らはクライミングを今後どう続けていけば良いのか
を書いてみようと思います。
まず前編はクライミングの話に入る前に、社会全体のシナリオを考えます。
なお断っておきますが、私は感染症の専門家でも医者でも予言者でもないのでここでの試算や見通しはあくまで素人考えです。
というか現時点でこの騒動がどうなっていきそうか、100%の確度を持ってわかる人間は世界に一人もいないと思いますが。
流行の推測
新型コロナの流行を推測する方法は色々とあるのでしょうが、一般的な感染症数理疫学で使われているであろうSIRモデルで考えます。
とはいっても計算式などは最小限にとどめて、考え方のフレームでなるべく説明していきます。
SIRモデルとは
緊急事態宣言以降はSIRモデルは一般ニュースでもだいぶ広まっているので聞いたことがある方も多いとは思いますが、基本的な考えだけでも説明しておきます。
総人口Nを、以下の3種類に分けます。
(短い期間ならばNは一定で、N=S+I+Rと仮定)
・S:感染する可能性のある人口(健康な人) susceptibles
・I: 感染していて感染させる能力のある人口(コロナにかかっている人) infectives
・R: 病気からの回復による免疫保持者、隔離者・死亡者(もうかからない人) recovered/removed
SとIとRは時間の関数であり日々刻々と変わっていきます。
・Sは、SとIが接触すればするほど日々減っていきます。(健康な人とコロナの人が接触すればするほど健康な人は減ります)
・Rも、Iが大きいほど日々増えます。(コロナにかかっている人が大きければ回復する人や死亡する人は増えます)
・Iは、Sの減った分だけ日々増え、Rが増えた分だけ減ります。
だとすると、
・感染率β(どのくらい接触するか、接触した際に感染者がどのくらい増えるかを決める係数)
・隔離率γ(どのくらいの期間で回復・死亡するかを決める係数)
という定数を導入してやることで、SとIとRの間に簡単なモデル式を立てることができ、それは解くことができるのです。
詳しく知りたい人はこの説明サイトやWikipediaなどを参考にしてください。
他にもネット上で検索すればいくらでも詳しいものが出ます。
またエクセルで簡単に組む方法もいくつかあります。
(僕もSIRモデルや感染症についてSIRモデルから学んだことを参考にして、エクセルを回しました。βやγの適切な設定が難しいですが)
基本再生産数R0・実効再生産数Rとは
このセクションだけ難しい数式を書くのですが、基本再生産数R0と実効再生産数Rは今後の見通しを考えるための超重要ファクターなのでそれぞれの意味合いだけでも把握すると話が分かりやすくなります。
基本再生産数R0
先ほどのSとIとRの間に式を立て、流行の初期という条件を付けてI(コロナにかかっている人の数)に関して解くと、
$$\bf I(t)=I(0)e^{βS(0)-γ}$$
が導かれます。
I(0)とS(0)は流行初期の「コロナにかかっている人」と「健康な人」の人数です。
これを日本語にすると、流行初期において、e(自然対数の底。ただの2.7くらいの数だと思ってOK)の指数となっている「βS(0)-γ」が正ならばI(t)は指数関数的に増加していくということです。
条件である
$$\bf βS(0)-γ>0$$
の形を変えると
$$\bf R_{0}=\frac{βS(0)}{γ}>1$$
となり、このR0を基本再生産数と定義します。
βS(0) は初期に1人の初期感染者が単位時間にどれくらい2次感染者を増やしてしまうか
1/γ は感染者が感染状態から回復や死亡する平均滞在時間
なので、
すなわち基本再生産数R0とは
感染者がその全感染期間の間に何人感染者を生んでしまうか
を意味することになります。
繰り返しますが、
R0 < 1ならば、eの指数が負になるので時間が経てばI(t)は自然に0となり感染は終息しますし、
R0 > 1 ならば、eの指数が正となり流行が連鎖的に拡大して感染者人口は指数関数的に増大します。
実効再生産数R
流行初期を過ぎると、
・既に感染し免疫を獲得した
・ワクチン等で免疫を得た
・隔離されて感染集団とは出会わない
などの人々が出てきます。
詳細な計算は省きますが、そのような人々の割合をpと置き
$$\bf R=(1-p)R_{0}$$
とすると、このRが1より大きいか小さいかでIが増加するか減少に転じるかを推測することができるようになります。
直感的に、例えばR0=2(1人が2人に感染させる)だとしても、pが0.5つまり50%の人々が免疫を持っていれば感染は広まらなさそうですよね。
計算式からもその時、
$$\bf R=(1-0.5)2=1$$
となり感染拡大は起こらないとなるのです。
とにかく、ここで言いたいことは注目すべき指標は基本再生産数のR0や実効再生産数のRであるということです。
日々メディアなどが
・感染者が何日連続何人超えだ
・死亡者数が何人に達した
・オーバーシュートがどうのこうのだ
などと報じますが、それらの数よりも現状Rはいくつくらいになってしまっているのかを考えることの方が本質的です。
Rが1を超えないということは、もし僕らが新型コロナウイルスに感染していたとしても、期間中に(どんなにどんなに妥協しても1人にしか)感染させてはいけないことになります。
このRを1未満にするために僕たちはどういった行動変容ができるのか、などを考えることが大切なのです。
(もちろん医療キャパなど、大局的には他にも重要ファクターはある)
流行の現状
現状の東京や日本、もしくは世界各国のR0やRはどの程度なのでしょうか。
この推定をしている人はいて、例えばTwitterの「uncorrelated」さんは東京ではR0は2.4程度であり何もしなければ9月に流行はピークを迎えてしまうとしています。
西浦先生も現状の日本のR0は2.5と動画でおっしゃっていて、だからこそ8割の行動削減をし実質的にp=0.8として、
$$\bf R=(1-0.8)2.5=0.5<1$$
とRを1未満にして感染拡大を防ごうと主張しています。
<東京のR0の推定>
<西浦先生の8割削減動画>
海外に関しては見立てが難しいです。
武漢で
・都市封鎖前:3.86
・都市封鎖後:0.3~1.58
(【図解】R0(基本再生産数)とは? 感染症疫学用語の基礎知識)
イタリアでもロックダウン後にRが1を切ったという記事もみます。
ただ基本的にRが1を切っていれば新規の感染者は減少に転じるはずなので、各国のデータを見る限りは都市封鎖レベルの措置やそれに匹敵するレベルの行動変容をしなければRが1を切ることは難しいと僕は考えています。
考え得るシナリオ
下準備が長くなったのですが、上記を踏まえ新型コロナウイルスが収束するシナリオを自分なりにいくつか考えてみます。
ただ収束の定義が難しいですよね。
ウイルスが完全にこの世からなくなれば文句なく収束(この場合”終息”が正しい?)ですが、皆がある程度社会的に落ち着けば新規に感染者がいても収束したと言えるはずです。
まぁここで収束を厳密に定義しても仕方がないので、今後社会がどういう方向に進みそうかを考えます。
1. 強力な接触制限で、R<1にする
理論上は日本でも、西浦先生の説明のように接触回数を60%以上減らせばR<1となっていつか収束します。
日経新聞の記事にグラフも載っていますが、70%削減(R0=2.5とすればR=0.75)でも潜伏期間を考慮しても2ヶ月程度で感染者が減少に転じるようです。
しかし、R=0.75というのは先ほどの議論だと都市封鎖のイタリアと同じ程度(かもっと厳しい制限)と推察されるので、この状態に日本を持っていくこと、そしてその状態をある程度の期間キープし続けるのは本当に難しいです。
もし完全に抑え込もうと思って感染者が0人になるまで接触制限を続け終息させる未来というのは僕はイメージがつきません。
ただ韓国は検査と合わせてこの方向を狙っているかもしれないし、中国、香港、ベトナム、ニュージーランド、あたりは上手くいっている可能性もあるのでありえないとは言い切れないです。
(ちょっと各国の状況はまだ調べ切れていないです)
2. 感染症が広まり集団免疫を獲得する
もう一つは例えば活動減少が間に合わずR>1でどんどん感染者が増えるのだけれど、途中で集団免疫を獲得し実質的にR<1となるというシナリオです。
例えばR0=2.5を用いると、pが0.6となったところで
$$\bf R=(1-0.6)2.5=1$$
となり感染の拡大は止まります。
このR=1となる時のpの値を集団免疫率と呼び、逆に計算すれば
$$\bf 1=(1-p)R_{0}$$
$$\bf p=1-\frac{1}{R_{0}}$$
と求めることも可能です。
ただこの方法はおそらくありえない、正確に言うと取るべきでないというのが僕の見方です。
例えば現状4/11の東京のデータを見ると、10万人あたり13.76人が感染者となっています。
すなわち東京の人口の0.014%程度しかまだ感染していないのです。
この状況ですら東京の医療キャパの限界は遠くないと言われているので、もし感染者の水準が60%に達したらそれは明らかに医療崩壊を避けられなかったシナリオであり、多数の死者が伴うと推測されるからです。
(正確にはトータルの感染者数ではなく、その瞬間に病院に入るべき人の数が大事だが、全体で60%に達しているなら計算するまでもなく医療キャパは超えているだろう)
もちろん、Rを1を少し超えるギリギリの水準に保ち限りなく流行のピークを遅らせて医療キャパも広げていき、結果的に集団免疫をみんなが獲得しましたよ、というシナリオは理論上はあり得るのですが、
・Rをそんな上手いバランスにキープできるのか疑問
・医療キャパもそこまで広がらない
という見方を僕はしてしまいます。
3. 医療キャパ内でワクチンを待つ
「R<1を続けてウイルスを撲滅する」「R>1で集団免疫を獲得する」の2つともあり得なさそうなシナリオだとすると、考えられるなかで最も現実味があるのは「上記2つの合わせ技+ワクチンによる免疫獲得 」ではないでしょうか。
似たような主張がモデリングから考える長期的なCOVID-19戦略という記事に書かれているのでそちらも読んで欲しいのですが、
・R<1となる強力な接触制限の期間
・R>1となってしまう現在程度の自粛期間
を繰り返すことで、なんとか医療キャパの崩壊はさせずに、経済活動も停止と再開の繰り返しつつそれぞれがwithコロナでも成り立つように業態を変更しながら、長期戦を取るというシナリオです。
そのようになんとか生きながらえながら、ワクチンの開発・実用を待ち、ワクチンの投与による集団免疫の獲得で収束を迎えるという見通しです。
ポジティブなシナリオですが、ビル・ゲイツは1年半後にはワクチンが流通するとも言及しています。
ただそれが日本人の60%近くに投与されるのは更に先になる可能性もありますし、ワクチン開発がそもそも上手くいくかはわかりません。
ただ僕は人類の科学の力を信じているので、遠くない未来いつかは必ずワクチンもしくは治療方法が完成すると思います。
<考えるうるシナリオ>
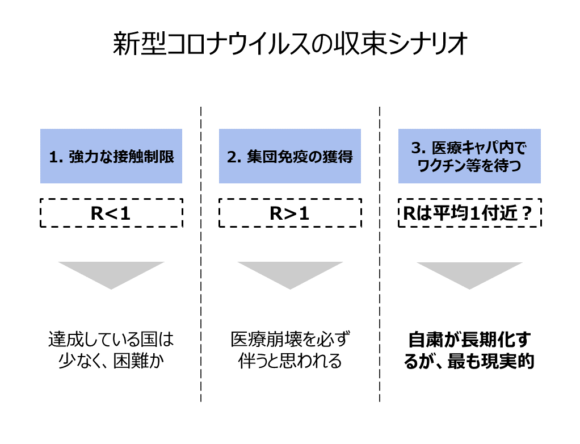
結論として僕としては、シナリオ3のような
「ワクチン普及までなんとか行動&社会システム制限で医療キャパを崩壊させないようにして、それまでの1.5~3年間程度は新型コロナウイルスと共に社会は回る」
というのが一番筋が良さそうな見通しだと考えています。
ハイブリットのシナリオ(例えば完全とはいかない集団免疫+ワクチン)や、もっと違うシナリオもあるとは思いますが。
後編ではいよいよメインである、
・クライミング業界はこの先どうなっていくのか
・僕らはクライミングを今後どう続けていけば良いのか
を考えていきます。
-
前の記事

自宅の壁に穴を開けずに、クライミングのフィンガーボードを設置した 2020.04.10
-
次の記事
“Withコロナ”の時代に僕らはクライミングとどう向き合うか 後編:クライミングの今後 2020.04.13
