カムはなぜ決まるのかを初等力学で考える 前編
- 2018.08.29
- データ&ルール 上達方法 岩場の記録 科学するクライミング
アメリカンデストライアングルの考察に続いて、初等力学で考えるシリーズ。
今回は「カムはなぜ決まるのか」。
<アメリカンデストライアングルの記事>
カムの構造をしっかり捉えようとすると少し難しい数学(といっても高校範囲)に入り込むのでそのあたりは後編に回し、前編ではカムが力学的にどういった力で作用するのかに焦点を当てます。
カムとは
カムとは、正式名称はSpring Loaded Camming Device(スプリング ローデッド カミング デバイス、SLCD)でバネが搭載されたアクティブプロテクションを指します。
要はクライマーの墜落を防ぐ少しメカニカルな道具です。
トリガーを引き写真のようにクラック等に差し込み歯がクラックに当たることでいわゆる”決まった”状態となり、カラビナにロープを通すことでクライマーの墜落を防ぐプロテクションとしての機能を果たします。
<家の戸に決まるカム>

アクティブプロテクションでないものとしてはナッツなどメカニカルな構造を持たず単に剛体ストッパーとして作用するパッシブプロテクションもあります。
(厳密にアクティブとパッシブに分けられないデバイスもありますが)
<絶対に墜落できないパッシブすぎるプロテクション>

カムにもさまざまな種類があり、メーカーやサイズによって
・歯の形状、大きさ
・歯の枚数(3枚か4枚か)
・左右の歯の軸は同じか(1軸か2軸か)
などが異なりますが、この記事では基本的な力学原理にフォーカスしたいのでそれらによる特徴の違いは一旦おいておきます。
ですので説明にはブラックダイアモンドのキャメロットX4を使い、簡略化する場合は1枚もしくは2枚の歯だけで話を進めますがどのようなカムに対してもほぼ同様に考えられるとして大丈夫です。
歯の形状
カムが決まる原理の根本となっているのはその歯の巧妙な形状です。
平行なクラックに決める場合、カムの歯の回転角度によらず「クラック」と「クラックとの接点へ軸中心から引いた直線」との角度が常に一定となるように作られています。
写真はキャメロットX4の0.4で二軸タイプなので、左側の軸(銀の丸)が見えている歯の回転軸となっています。
この性質は歯が対数螺旋と呼ばれる形状になっていることに由来するのですが、数学的な説明は後編で触れますのでこの記事では上記の性質があることを認めて話を進めていきます。
<歯の回転角度によらず角度一定>

カムにかかる力
ではいよいよカムがなぜ決まって墜落を支えることができるのかを考えてみましょう。
地面に対して垂直かつ2つの平行なクラック(図の黒線)にカムが決まっている状況を考えます。
歯の回転角度によらず「クラック」と「クラックとの接点へ軸中心から引いた直線」との角度が常に一定なので、その角度をαと置きます。
このαはクラックが平行である限りはカムのトリガーをどの程度引いて歯を回転させようと同じカムならばいつでも一定ということです。
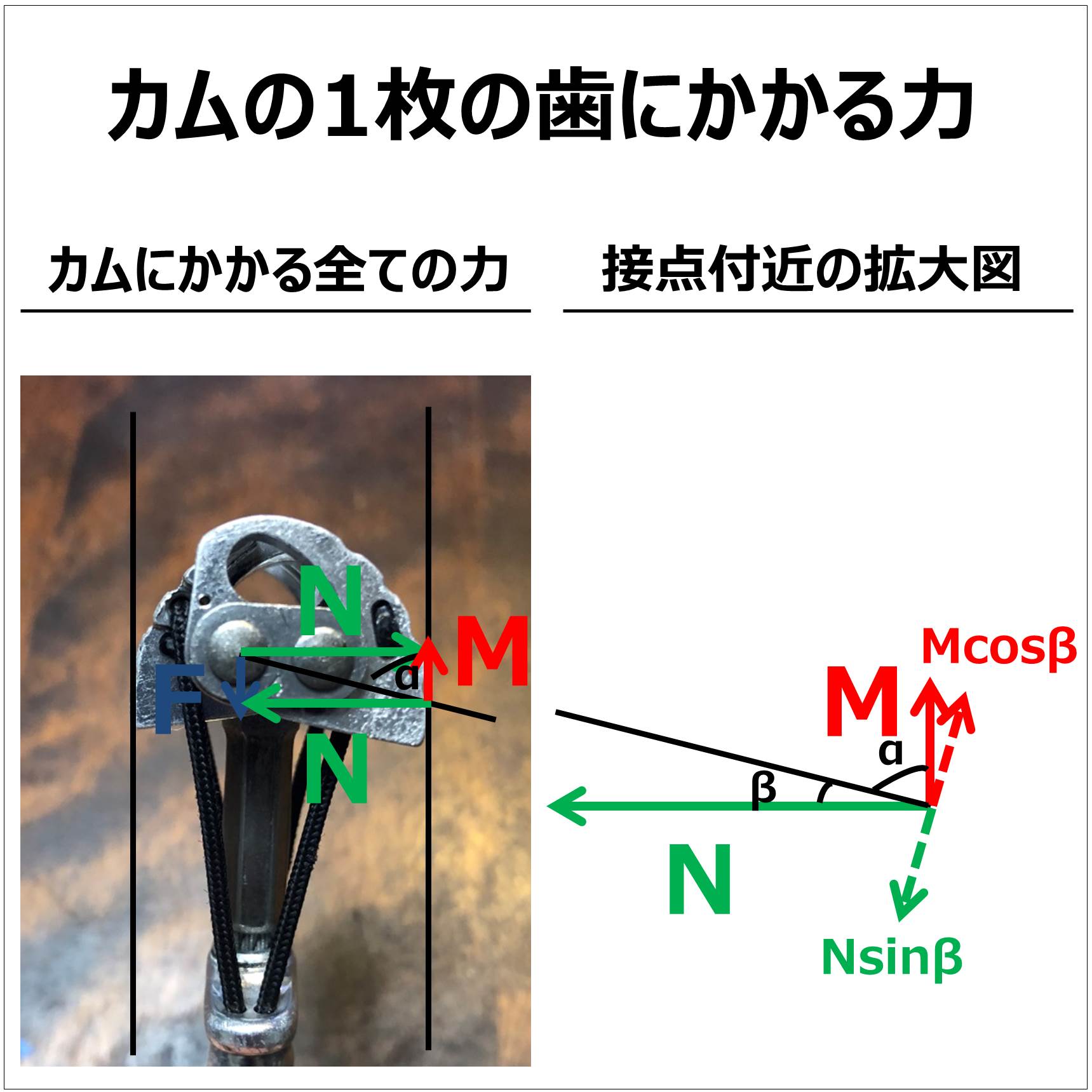
簡単のため1枚の歯についてだけ考えます。
墜落や荷重時にカムにかかる力をF(4枚歯のカムならば合計4Fで下方向に引かれます)
クラックから1つの歯にかかる力の垂直抗力をN、摩擦力をMとおきます。(4枚歯ならそれぞれ全体で4つのNと4つのMがかかっている)
水平方向にはカムは動かないので力の釣り合いから軸にも右方向へNの力がかかっています。
そしてこの絵からわかることはαが常に一定に保たれ垂直抗力が発生しそれが摩擦力Mを生み出しそれがカムを支えているということです。
もしこの性質がなく、クラックと歯の接点が軸よりも高いところにきてαが90°を超えてしまったら力Fがかかっても摩擦力Mは生じません。
ですのでバネが開く力がカムを支えているというような記述をたまに見かけますがそれは少し誤解を招く表現ですね。
カムが決まったまま滑らない条件を考えてみましょう。
カムは静止しているので垂直方向の力の釣り合いから
$$F=M$$
また、カムは回転もしていないので歯にかかる力のモーメントも一定なはずです。
軸まわりのモーメントを考えて、軸中心からクラックとの接点へ引いた黒い直線と水平線の角度をβ(α+β=90°)とおくと、摩擦力Mと垂直抗力Nが歯に与えるモーメントはそれぞれ釣り合うので、
軸から接点までの長さをLとすれば
$$LMcosβ=LNsinβ$$
より
$$M=Ntanβ$$
そして滑り出す直前の最大摩擦力をM’とすると、歯とクラックの間の静止摩擦係数をμとして、カムが決まっていて滑り出さない限りは
$$F<M’=μN$$
が満たれる。これに上記の2式を代入すると
$$Ntanβ<μN$$
すなわち、カムが滑らない条件は
$$tanβ<μ$$
となります。
カムが決まる条件の考察
さてカムが滑らない条件が
$$tanβ<μ$$
という結論から何がいえるのでしょうか。
決まったままかどうかはカムにかかる力によらない
$$tanβ<μ$$
という式には力Fが入っていません。
そして最初に述べたカムの歯の形状より、βはカムによって固有の値であり、
μも歯の素材とクラックの素材から決定される静止摩擦係数です。
つまり、地面と垂直な平行クラックに決める場合、カムが壊れない・歪まない、クラックが欠けない限りは、滑るかどうかはカムにかかる力によらない、ということが言えるのです。
ちなみにキャメロットの場合βは14°程度、フレンズなどの場合は13.75°程度に設定され、この角度はカムアングルなどと呼ばれます。
花崗岩に決める場合、μは0.5程度となるらしいので
$$tan14°≒0.25<0.5$$
が常に満たされることがわかります。
ですので理論上はカムやクラックが歪まず壊れない力の範囲内ならば、地面と垂直な平行なクラックに決めればカムが滑ることはないのです。
角度βはなぜ0に近い値ではないのか
ではなぜβは14°付近に設定されているのでしょうか。
詳しいことは参考文献を読んでほしいのですが、以下僕の理解を書きます。
まず、βが大きい値だとまずいことは
$$tanβ<μ$$
という条件からわかります。
なぜならtanβは0°~90°で単調増加なので、βが90°に近づくとあるところでμを越えてカムが滑ってしまうからです。
それならばβは限りなく0°に近ければ、μが小さいとき(花崗岩ではないツルツルのクラックのとき、岩が濡れていて摩擦係数が下がるとき)でも安心してカムを決められるので都合が良いように思えます。
しかし実はβは小さすぎてもダメなのです。
理由の1つ目としては、βが小さすぎると平行よりも開いた(フレアした)クラックにカムを決める場合に対応できないからです。
例えば以下の絵のように両側のクラックがそれぞれβだけ垂直方向からフレアしたクラック(赤線がクラック)を考えます。

するとカムの軸からクラックとの接点へ引いた緑の直線が水平になってしまい、もしこれ以上クラックが傾いたらカムに力がかかっても摩擦力を得られないことがわかります。
実際にはここまでフレアしていなくても、クラック表面の凹凸だったり、カムの歯が変形していたりして、実質的に上記の絵と同じような状況になってしまうこともあるので、ある程度βには余裕がないと摩擦力が生じないケースが起こり得るのです。
2つ目の理由としてはβが小さすぎるとカムの歯にかかる垂直抗力がとてつもなく大きくなってしまうからです。
先ほど述べた式変形より
$$N=\frac{F}{tanβ}$$
なのでβが小さければ小さいほどクラックから大きな力をカムは受けることになります。
これが摩擦力を生み出している源泉なのですが、βがあまりに小さいとカムが壊れるほど大きな垂直抗力が働いてしまいカムがその構造を維持できなくなってしまうと考えられるのです。
同様の力でクラックを押すのでクラックが欠ける可能性も高まります。
トリガーは50%以上引く必要はあるのか
カムを決めるときにトリガーを50%~90%の範囲で引いて決めると良い、と一般的に言われています。
ブラックダイヤモンドの日本語取扱い説明書にも”全てのカムが50〜90%閉じた状態で岩に接し”と書いてあります。
90°以上引いてはいけない理由はカムが完全に引かれた状態で岩にスタックしてしまい回収不能となるリスクを避けるためだと思われます。
しかし50%の方は、これまでの議論からトリガーをどれだけ引こうともカムの歯の回転角度によらず「クラック」と「クラックとの接点へ軸中心から引いた直線」との角度が常に一定(すなわちαやβが一定)なので、理論上は1%でもトリガーが引かれていればカムは決まるはずです。
ではなぜ50%は引いた方が良いとされているのかというと、現実にはカムは歪むし、クラックも平行ではなく場所によって幅が違ったり表面に凹凸があるからだと思います。
例えば1%しかカムを引いていない状態でクラックにカムを決めた際にカムがその1%分だけ歪んで完全に開いてしまったり、クラックの幅が広いところに動いてしまい同じく完全に開いてしまったりして、摩擦力を得られないというケースは起こります。
ですので安全マージンをとって50%くらいは引いておこうとなっているのでしょう。
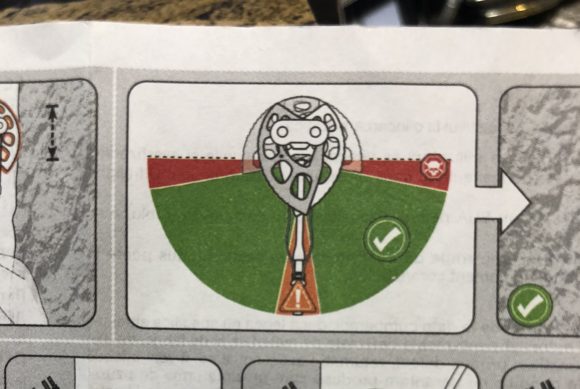
ちなみにウェブ上ではなく製品付属の英語版のキャメロットの説明書だと50%よりも大分小さい確度でも安全となっていますね。(図の緑)
<付属のキャメロット説明書>
終わりに
クラックをやるようになって当たり前のようにカムを使っていましたが、正直な話その原理は深くは理解しないままでした。
好奇心から調べてみましたが、カムの構造や決まる原理が自分なりに腹落ちしカムを扱う安全上もとてもためになりました。
後編ではもう少しマニアックなカム歯の形状の数学的特徴を扱います!
参考文献
日本語の本では『イラストクライミング』にカムアングルや対数螺旋の話が載っています。
<イラストクライミング>
あとは以下の英語のウェブ文献が役に立ちました。
というか僕の議論よりも詳しいです。
読み切れていない箇所も多いですが。
Spring Loaded Camming Device for rock climbing analysis and optimization
An Elastic Model of the Holding Power of Spring Loaded Camming Devices Used as Rock Climbing Anchors
-
前の記事

中国陽朔クライミングトリップ~喧噪の観光編~ 2018.08.21
-
次の記事

カムはなぜ決まるのかを初等力学で考える 後編 2018.08.31
