スポーツクライミングコンバインド「2種複合」の新ルール 第4回CJC 2021年6月時点

今週末の2021年6月18,19日（金,土）は岩手県営運動公園スポーツクライミング競技場にて第4回コンバインドジャパンカップ（以下CJC）が行われます。
僕も18日の予選をJMSCAチャンネルで実況解説をするので、皆さんよろしくお願いします。

この大会は2024年のパリオリンピックの強化選手の選考にもなっています。
そのため東京オリンピックのフォーマットではなくパリオリンピックを想定したフォーマットで競われ、ルール等がこれまでとかなり変更されています。
選手達はもちろんのこと観戦する方々にとっても新ルールをしっかりと把握しておくことは大切なので、このブログでは詳細に変更点を解説しYouTubeの方ではざっくり要点を話します。

＜CJC新ルール YouTube解説＞

ルール原文&前提

この記事は以下の2つに書いてあることをほぼまとめ直しているだけなので、一次情報できちんと把握したい方は原文を読んで下さい。
・JMSCAの競技規則「JMSCAスポーツクライミング競技規則」の「第12章 コンバインド（ボルダリング/リード）」
・スポーツクライミング第4回コンバインドジャパンカップ　コンバインド（ボルダリング/リード）種目　ルール概要

また非常に重要な前提なのですが、今回の新ルールは「第17回IFSC総会（2021年4月）ワーキンググループ答申）」を元に日本側で作成したものであり、パリオリンピックに向けた暫定的な2種複合のルールです。
3種複合ルールも
・決勝メンバーが6人→8人
・決勝のボルダリング課題が4課題→3課題
など後からルールの変更はいくつかありました。
同様にこの2種複合の新ルールもパリオリンピック開催まで3年以上あるため、今回のCJCでのフィードバックを元に今後細部がブラッシュアップされていくでしょう。
なのであくまでもこれから説明するものは、現時点での2種複合ルールで今後変わり得るものだと理解しておきましょう。

新ルールの大まかな変更点

まず初めにコンバインドの新ルールの大まかな変更点を説明すると以下になります。

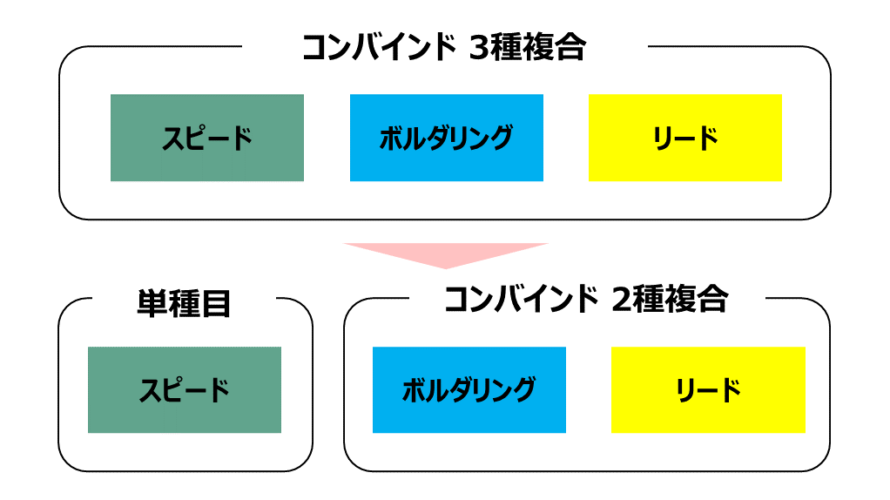
1. 「スピード」が無くなり「ボルダリング」と「リード」の2種複合に

2. 総合成績の評価が「順位の掛け算」ではなく「ポイントの足し算」に。ポイントは基本的には以下で決まる
　・ボルダリング：「トップ数」「ゾーン数」の多さ、「トップアテンプト数」「ゾーンアテンプト数」の少なさ
　・リード：「高度」の大きさ

ルールブックを既に読んだ方は、新ルールはかなりややこしいと感じているのではないでしょうか。
しかし実際のところはボルダリングとリードそれぞれの種目内での成績の付き方ではほぼ変更点は無く、それぞれのポイントを合算するための計算処理が複雑化しているだけなのです。

＜スポーツクライミングの枠組み変更＞

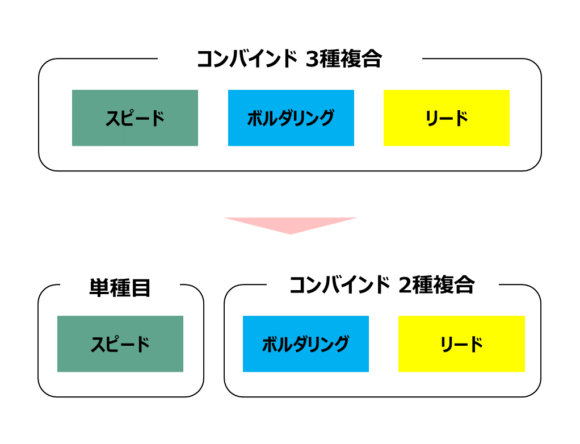
変更点1 . スピードが無くなり、ボルダリングとリードの2種複合に

最大の変更点は、スピードがコンバインドから外れ2024年のパリオリンピックは「スピード単種目」と「ボルダリングとリードの2種複合のコンバインド種目」となることです。

東京2020オリンピックにスポーツクライミングが選ばれて以降、コンバインドは「スピード」「ボルダリング」「リード」の3種複合形式でおこなわれてきましたが、このフォーマットはどうやら東京オリンピックが最後になりそうですね。
元来、速さを競う「スピード」と難易度（ディフィカルティ）を競う「ボルダリング」や「リード」は競技の性質やプレイヤー層も違っていたため、3種複合のフォーマットが発表された際には多くのクライマーから疑問の声が上がっていました。
しかし今となってはスピードの決着の明快さや疾走感はクライミングの楽しさを一目で理解できる良い種目でもあるとも感じるので、いざコンバインドから外れると少し寂しさもあります。

変更点2. 総合成績の評価がポイントの足し算に

コンバインドの成績評価方法は従来の「順位の掛け算」ではなくなり、「ボルダリングとリードのそれぞれでポイントを算出しそれを足し算する」というものに変更されます。

まずこのルール変更の背景を説明します。

2種複合で順位の掛け算をすると同成績になりやすい

上記の「ルール原文」のリンク先にも書いてあるのですがまず第一に、
・2種複合で順位の掛け算をするとタイ順位が出る可能性が高い
という背景があります。

決勝の8人で2種複合で掛け算によって成績を決めるとしましょう。
すると例えば、（B=2位,L=6位）、（B=3位,L=4位）、(B=4位,L=3位）、（B=6位,L=2位）の選手たちは全て12ptとなりタイ順位になります。
ちなみに計算したところ、順位の掛け算結果の種類は
・3種複合：1pt（1位×1位×1位）から512pt（8位×8位×8位）まで80種類
・2種複合：1pt(1位×1位）から64pt（8位×8位）まで30種類
となるので、2種複合は確率的にも同ポイントがかなり出やすくなります。

さらに、3種複合では「掛け算が同じになったときは、3種目それぞれの順位を1つ1つ突き合わせて勝ち数の多い方が上位」というルールがありましたが、2種複合だとそのルールを適用することもできません。
（例：3種複合では（S=3位,B=4位,L=1位）のA選手と、（S=1位,B=3位,L=4位）のB選手はともに12ptだが、スピードとボルダリングの2種目で順位が高いB選手が上位となった）

ボルダリングの順位をパッと見でわかるように

また明言されているわけではありませんが、ボルダリングにおいて「トップ数」「ゾーン数」「トップアテンプト数」「ゾーンアテンプト数」から選手の順位を判断することは、一般の視聴者からするとおそらくかなりややこしいです。
そこで本質的には全く同じなのですが、トップを取ったら〇pt、ゾーンを取ったら△ptというように、パフォーマンスをポイント化しパッと見て順位がわかるようにしたという背景もあるようです。

このあたりはアメリカの公式ボルダリング大会に近いイメージで、アメリカの場合は、完登で25pt、ゾーンが3つあり達したところによって5pt、10pt、15pt、が入るというルールになっています。

＜2019 USA Climbing: Bouldering Open National Championships | Finals＞

2種複合の新ルール詳細

前置きが長くなりましたが、ここから具体的に2種複合の新ルールを解説します。
まずは新ルールの全体概要図を貼りますが、いきなり理解することは難しいので以下1つ1つ説明していきます。

＜コンバインド（ボルダリング/リード）種目　新ルール全体図＞

全体を通じた基本的な考えは、
・順位ではなく選手のパフォーマンスをポイントに反映
・ボルダリングとリードの種目間での難易度が選手の成績に影響しづらくするために、規格化をして（1位の人を100点に合わせて）から足す
となるので、この2点を頭に入れておくとルール上の計算処理の意味などが呑み込みやすいかと思います。

①パフォーマンスポイントの算出 ボルダリング

ではボルダリングから。
基本的な形式はこれまでと全く同一です。
予選：4課題。単種目の準決勝と同じ方式（ベルトコンベア）
決勝：3課題。単種目の決勝と同じ方式（W杯決勝方式）

基礎ポイント

選手にはトップ数とゾーン数に応じて以下の基礎ポイントが入ります。
■予選
　・トップ数×25pt
　・ゾーン数×5pt
■決勝
　・トップ数×33pt
　・ゾーン数×8pt

この時トップを取っている課題に関してはゾーンとトップのポイントが重複して入ることはなく、例えば予選ならば1つ完登したら25pt+5ptの30ptとはならず25ptのみが入ります。

この得点振り分けの背景には全完登した選手のポイントをほぼ100ptにするという考えがあるようで、全完登すると
・予選：25pt×4課題で100pt
・決勝：33pt×3課題で99pt
となります。

また従来のルール通り、1つトップを獲得した選手の方が、0トップ全ゾーン獲得の選手よりも上位に評価されるべきであり、その点に関しても
■予選
　・1トップのみ：25pt
　・0トップ全4ゾーン：20pt
■決勝
　・1トップのみ：33pt
　・0トップ全3ゾーン：24pt
と順位が入れ替わることは基本的にないような設定になっています。

タイブレイク

トップ数とゾーン数のみ考慮する基礎ポイントだけでは、当然ながら同ポイントの選手が複数名出る可能性は高いです。
そこで基礎ポイントが同じ選手が出た場合はタイブレイクとして、
・トップ獲得にかかったアテンプト数×0.1pt
を基礎ポイントから差し引きます。

例えば、
・A選手：3完登3ゾーン トップアテンプト数が3
・B選手：3完登3ゾーン トップアテンプト数が5
だった場合、基礎ポイントは両選手とも25pt×3完登の75ptです。
よってタイブレイクとなり、
・A選手：75pt – 3アテンプト×0.1pt＝74.7pt
・B選手：75pt – 5アテンプト×0.1pt＝74.5pt
とポイントが差し引かれ、トップのアテンプト数がより少ないA選手の方が上位になります。

トップのアテンプト数を考慮してもなお同ポイントであった場合さらなるタイブレイクが適用され、
・ゾーン獲得にかかったアテンプト数×0.01pt
を同様に差し引きます。

このタイブレイクまで適用した後のポイントを「パフォーマンスポイント」（ボルダリングならボルダリングパフォーマンスポイントでBPPと略される）と呼びます。

タイブレイク後もなお同ポイントだった場合、これ以上の処理はコンバインドでは行わず同ポイントのままとします。
（ボルダリング単種目の決勝ではカウントバックを適用しても表彰台に関わる選手が同成績の場合は、1撃完登したボルダー数の比較、2撃完登したボルダー数の比較、、、などとしていくが、コンバインドではその処理はなされない）

ポイント化する影響は？

ここまでで何やら難しいことをしていると感じる方もいるかもしれませんが、「トップ数」＞「ゾーン数」＞「トップアテンプト数の少なさ」＞「ゾーンアテンプト数の少なさ」の順で順位に影響するという意味では従来ルールと変わりはありません。

しかし、新ルールではそれぞれがポイント化されたことによって順位以上にパフォーマンスの中身がどうだったかということが成績に影響を与えます。
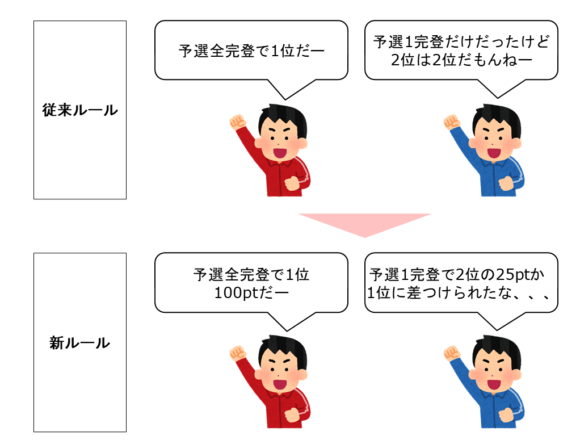
例えばこれまでなら予選で1位が全完登のとき、2位の選手のパフォーマンスが3完登でも1完登でもどちらも結果として2位ならばその2という数字が最終的な成績を決める掛け算に使われるため、パフォーマンスは成績に影響はありませんでした。
これが新ルールの場合では1位は全完登の100ptを得ますが、
・3完登で2位だった：75pt
・1完登で2位だった：25pt
と同じ2位でもパフォーマンスによってポイントに大きく差が出ます。
ここでのポイントを元にしてリードとの合算で総合成績が付くため、順位以上に自分の登りのパフォーマンスがどうであったかということが成績に影響すると言えるでしょう。

＜従来ルールと新ルールでの違いの例＞

①パフォーマンスポイントの算出 リード

リードも基本的な形式はこれまでと同一で、予選決勝ともに1ルートのオンサイト形式で実施されます。

リードパフォーマンスポイント LPP

リードのポイント形式はボルダリングよりもシンプルであり、予選決勝ともに
・高度×2.5pt
・+判定は0.5ptが追加
となります。
完登した場合は「最終ホールドの高度に+1をしたものを獲得高度と見なす」ので、例えば最終ホールドの高度が50のルートを完登したら
・51×2.5pt=127.5pt
を選手は得ることになります。

なぜ2.5ptなのかというと、こちらもボルダリング同様に完登した選手のポイントをだいたい100ptにしたいという思惑があるようです。
100pt÷2.5pt＝40となることより、平均的なルートの手数である40手と一致するというわけです。

このポイントをボルダリングと同様にパフォーマンスポイント（リードなのでリードパフォーマンスポイントでLPPと略される）と呼びます。

リードも高度がそのまま成績に直結するので、リードの中での順位付けに関しては従来のルールと変わりはありません。
しかしボルダリング同様に、同じ順位でも、
・高度いくつまで進んだのか
というパフォーマンスがポイント化されることで成績に反映されます。
逆に言うと、+差などで順位に差が付いてもポイント上では0.5ptしか変わらないため、多くの選手が固まってしまう団子地点から抜けることの価値は以前よりもしかすると下がったのかもしれません。

タイムが無くなった

従来との決定的な違いに、
・リードにおいて、（6分間以内ならば）タイムの速さが成績に影響しない
というルール変更があります。

リードの単種目ではタイムは決勝の表彰台に関わる選手に対して最後に順位に差をつけるためだけに用いられていました。
しかしコンバインドのリードではタイ順位を避けるために、同高度の選手が出た場合常にタイムが速い選手を上位としていました。
そのため速く登るということがコンバインドのリードでは戦略上非常に重要でしたが、新ルールではタイムが全く影響しなくなったため速く登る必要性が下がったと言えるでしょう。

こちらも背景としては、リードという難しさへの対処や持久力の有無を競う種目にタイムという概念をなるべく持ち込みたくはないというIFSC側の思惑があったと予想されます。
しかしコンバインドではタイムの導入によってこれまでタイ順位の解消が成されてきたことは否めないため、新ルールでリードの同高度がたくさん出るようであればもしかすると今後タイムを再度導入する流れになるかもしれませんね。

②ステージポイントへの規格化 （ボルダリングポイントBPとリードポイントLP）

ここまででボルダリングとリードのそれぞれでパフォーマンスポイントが算出されたわけですが、これらをそのまま足し算すると若干の問題が生じます。
なぜかと言えば、パフォーマンスポイントにはボルダリングとリードの課題やルートの難易度が大きく影響を与えてしまうからです。

選手のポイントをなるべく相対化する

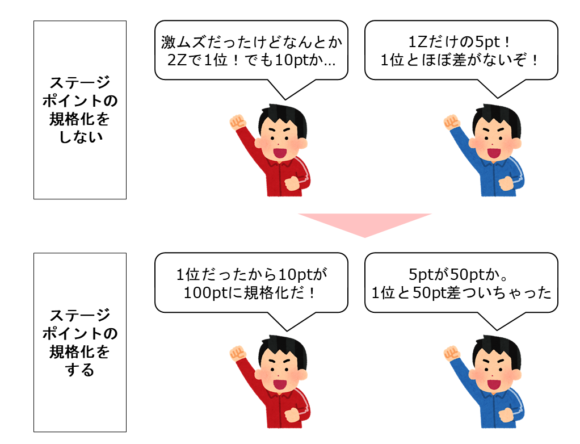
例えば予選のボルダリングがものすごく難しい設定になってしまい、1位の選手ですら2ゾーンしか獲得できなかったとしましょう。
このとき、以下を仮定します。
・A選手：2ゾーンで1位だが、ボルダリングパフォーマンスポイント（BPP）は10pt
・B選手：1ゾーンでBPPは5pt
ここでこのままパフォーマンスポイントをリードとの足し算に使用する、1位のA選手とB選手に5ptのみの差つまりリードにおいて2手分の差にしかつきません。
こうなるとコンバインドであるにも関わらず、ほぼリードの成績で勝負が着く展開となります。
ボルダリングではたしかにA選手も2ゾーンしかとれなかったわけですが、非常に厳しい設定の中で1ゾーンであるB選手よりある意味2倍のパフォーマンスを見せたのに、実力差が成績にほぼ反映していないわけです。
それよりは、選手間での相対的なパフォ―マンス差をポイントになるべく反映させてからボルダリングとリードで足し算した方が、コンバインドという2種複合では健全な評価方法だと言えます。

ステージポイントの具体的な計算方法

この問題を解決するためにステージポイントという概念を導入します。
ステージポイントの計算方法はボルダリングとリードそれぞれで、以下となります。
■PPが1位の選手のポイントを100ptとするように調整する
　具体的には、
　・ボルダリングステージポイント BP = BPP×100÷1位の選手のBPP
　・リードステージポイント LP = LPP×100÷1位の選手のLPP

このようにある選手の点数を100にして他の選手にもそれと同じだけ係数をかけることを（正式用語ではないが）規格化と呼び、この一連の操作を「ステージポイントへの規格化」と命名させていただきます。

先ほど出したボルダリングの例だと、パフォーマンスポイントの段階では
・1位のA選手のBPP：10pt
・B選手のBPP：5pt
だったわけですが、A選手は1位なのでボルダリングステージポイントBPが100ptへと規格化されます。
そしてB選手も
・B選手のBP = 5pt×100÷A選手のBPP10pt =50pt
と規格化されます。（要はA選手と同じだけ10倍された）
これによってA選手とB選手は50ptの差、つまりリードの20手分の差が付くことになります。
このケースでは他の選手のBPも同じだけ10倍されステージポイントへと規格化され、A選手を100ptとしたときに各選手の相対的なパフォーマンスがステージポイントとして表されたと見ることができるのです。

リードにおいても全く同様に1位の選手のLPが100ptとなるようにステージポイントへ規格化をします。
リードの場合は40手を超えるルートだとパフォーマンスポイントが100を超えるケースもあるので、規格化によってポイントが下がることも起こり得ます。

＜ステージポイントの規格がある時とない時＞

③複合ポイント

最後に②で出てきた2つのステージポイントであるBPとLPを足し算し、
・複合ポイント=BP+LP
によって順位を着けます。
予選では複合ポイントの上位8名が決勝へ進出しますが、複合ポイントが同一で上位8名に絞れない場合は対象選手全員が決勝へいきます。
決勝では複合ポイントが同一であった場合は予選の複合順位へのカウントバックをおこない、なお同一であった場合は同順位となります。

新ルールへの所感

コンバインドの新ルールの説明は以上となりますが、いくつか僕自身の所感を述べておきます。
結構想像も交えて突っ込んでいるので、興味のある方だけ読んでみてください。

ステージポイントで規格化されるとはいえ、種目間難易度の影響は排除できない

この新ルールではステージポイントの規格化によってボルダリングとリードの難易度差はある程度均されますが、それでも成績への影響は大きいと感じました。
例えば、ボルダリングの課題が易しめで全完登のアテンプト勝負になり、A～Dの4選手が以下のように並んだとします
・A選手：4完登4アテンプト
・B選手：4完登6アテンプト
・C選手：4完登10アテンプト
・D選手：4完登14アテンプト
この時、基礎ポイントはいずれの選手も100ptです。

よってタイブレイクとなりアテンプト数×0.1ptだけ差し引かれるので、各選手のBPPは
・A選手：100 – 0.4 = 99.6pt
・B選手：100 – 0.6 = 99.4pt
・C選手：100 – 1.0 = 99.0pt
・D選手：100 – 1.4 = 98.6pt
となります。

さらに首位のA選手を100ptにするようにステージポイントへの規格化をするため、各選手のBPは
・A選手：100pt
・B選手：99.4×100÷99.6 = 99.799pt
・C選手：99.0×100÷99.6 = 99.398pt
・D選手：98.6×100÷99.6 = 98.996pt
となり、結局のところA選手とB選手は約0.2ptの差、A選手とD選手でも約1ptの差にしかならないことがわかります。
ボルダリングをやっている人やコンペをよく観戦している人の感覚からすると、全完1撃の選手は全完6アテンプトや14アテンプトの選手と比べるとパフォーマンスとしては頭一つ上だったなという印象を得ると思います。
何より従来のルールではA選手は1位、B選手は2位となり、掛け算で使う数字に2倍の開きが出ていました。
ですが計算してみるとA選手とB選手の差はリードの+の差以下であり、D選手との差もリードの1手で逆転してしまうものに過ぎず、ほぼリードで決まるコンバインドになってしまうのです。
またここから1位を取ることの旨みがだいぶ減ったとも言えるかもしれません。

逆にリードにおいて全選手のフォールポイントが上部に固まった時などは、リードでのパフォーマンス差がほぼ影響されずボルダリングのゾーン差で決まってしまうなどが起こるとも考えられます。

それ故にいくらステージポイントへの規格化があるからといって、ボルダリングとリードそれぞれで選手のパフォーマンスポイントがそもそも綺麗に分かれるようなリザルトにならないとどちらか一種目でコンバインドが決まる状況になり兼ねないとわかります。
セッターに対して、ただ単にリザルトを分けるだけでなくパフォーマンスポイントがばらけることまで求めるのは厳しい注文ではありますが、確実に配慮が必要な点でしょう。

ボルダラー有利？

かなり直感が入るのであくまでただの推測として聞いて欲しいのですが、新ルールではボルダリングに強みを持っているいわゆるボルダラーの方が少し有利な成績になるのではないかと予想しています。
というのも例えば決勝において規格化前では、ボルダリングの1完登である33ptはリードの13手分以上に相当します（13手×2.5pt=32.5pt）。

（データに基づいて出しているわけではないので感覚で申し訳ないですが）ボルダリングだと1完登差なら実力が僅差と見なすこともまぁまぁあるのに対して、ルートによるのですがリードで13手～14手の差が付くというのは「核心2つ超えたくらいの差」に感じることが僕は多いです。
ステージポイントへの規格化があるのでトップ選手のパフォーマンスによりますが、なんとなくボルダーの1完登の差で勝敗が決着することが多いんじゃないかなーと感じます。
何度も繰り返しますがドタ勘です。

例として去年の第3回コンバインドジャパンカップの男子決勝に新ルールを当てはめてみました。
あまりに複雑なので計算式は省き小数点も第1位までしか出しませんが、男子のボルダリングでは規格化後のBPは以下になります。
1位 藤井選手：2T 3Z 2TAt = 100pt
2位 土肥選手：2T 3Z 4TAt = 99.7pt
3位 竹田選手：2T 2Z = 89.4pt
4位 樋口選手：1T 3Z = 66.4pt
5位 今泉選手：0T 3Z 3ZAt =32.5pt
6位 清水選手：0T 3Z 7ZAt =32.4pt
7位 百合草選手：0T 1Z 1ZAt =10.8pt
8位 大政選手：0T 1Z 3ZAt =10.8pt
まずこの段階で、1完登している4位の樋口選手ですら66.4ptと首位の藤井選手に33.6pt差が付いてしまいリードでの挽回が非常に難しそうです。

そしてリードの高度とLPは以下となります。
1位 樋口選手：Top（44として計算） = 100pt
1位 清水選手：Top（44として計算） = 100pt
3位 藤井選手：42+ = 95.9pt
4位 今泉選手：41+ = 93.6pt
4位 百合草選手：41+ = 93.6pt
4位 土肥選手：41+ = 93.6pt
7位 竹田選手：29+ =66.4pt
8位 大政選手：16 =36.4pt
よくある展開の最終局面勝負となったケースで、41+以上進んだ6名の選手が93.6ptから100ptの6.4pt内に固まっている状況です。

このBPとLPを足し合わせた複合ポイントと順位は、以下となります。
1位 藤井選手：195.9pt
2位 土肥選手：193.4pt
3位 樋口選手：166.4pt
4位 竹田選手：155.8pt
5位 清水選手：132.4pt
6位 今泉選手：126.1pt
7位 百合草選手：104.5pt
8位 大政選手：47.2pt
結局ボルダリングで2完登した藤井選手と土肥選手を他の選手はリードでは挽回できなかった結果となります。
これが順位の掛け算を用いた場合であれば、
・藤井選手：3pt（1位×3位）
・土肥選手：8pt（2位×4位）
・樋口選手：4pt（4位×1位）
となりリードで1位を取った樋口選手に逆転の目はあったのですが、やはり新ルールではリードである程度トップに近い高度にどの選手も達してしまうとボルダリングの影響が大きくなってしまうのかもしれません。

ただたまたま前回のコンバインドジャパンカップがボルダリングで完登数の差が付き、リードは多くの選手がトップに近い高度に達していたからこのような結果になったわけであり、ボルダリングが簡単でリードが下部からバンバン落とされるようなルートであれば逆のことが起きるとは思います。
なのでこのシミュレーションをもってしてボルダラー有利は少し言い過ぎなのかもしれません。

ボルダリングで「1トップ」が「0トップ」に負ける！？

最後はほぼお遊びの小ネタ。
ボルダリングで基礎ポイントが同一の場合は、タイブレイクとしてトップのアテンプト数×0.1を差し引くと書きました。
では以下のような極端な場合がもし生じたらどうなるでしょうか。
・A選手：1完登 1ゾーン 完登アテンプト数1
・B選手：1完登 1ゾーン 完登アテンプト数51
・C選手：0完登 4ゾーン
この時A選手とB選手の基礎ポイントは25ptで並ぶのでタイブレイクが生じます。
C選手の他に0完登4ゾーンの選手がいなければ、C選手は基礎ポイント20ptから何も引かれません。
よってBPPは、以下になります。
・A選手：25pt – 1×0.1 = 24.9pt
・B選手：25pt – 51×0.1=19.9pt
・C選手：20pt
つまり、B選手のように同じ課題に51アテンプト以上するケースが生じた場合は、1完登の価値を4ゾーンが上回ると言う怪奇現象が起きるのです。

まぁほぼ起きることはないので無視してください。笑


非常に長くなりましたが、以上で終わります！