クライミングの衝撃荷重はなぜ落下係数で決まるのかを初等力学で考える　中編

ロープを使ったクライミングで落下した場合、衝撃荷重はなぜ落下距離などではなく落下係数で決まるのかを初等力学で考える、の中編。
前編では、
・落下係数や衝撃荷重などの言葉の定義や説明
・衝撃荷重が落下係数で決定するという意味
・今後の議論の前提や注意点
を書きました。

実際に式を導出する前に、この中編では必要となる物理や数学の「武器」を少し丁寧に説明します。
全てを原理から説明する時間はないので、ある程度は「そういうものなんだな、ふんふん」と捉えてもらって構いません。

＜前編＞

フックの法則

まずは最も理解してほしいフックの法則について。

バネは伸ばすと縮もうとし、縮めると伸びようとします。
このような力を弾性力や復元力と呼び、理想的なバネでは弾性力はバネの伸び分や縮み分に比例すると考えることができます。
すなわちバネの伸び分をx（m：メートル）とするとこの弾性力F（N:ニュートン）は

$$F=kx$$

と書くことができます。
k（N/m）はバネ定数と呼ばれるもので、バネによって決まるただの数だと思ってもらって構いません。
上の式を「フックの法則」と呼びます。

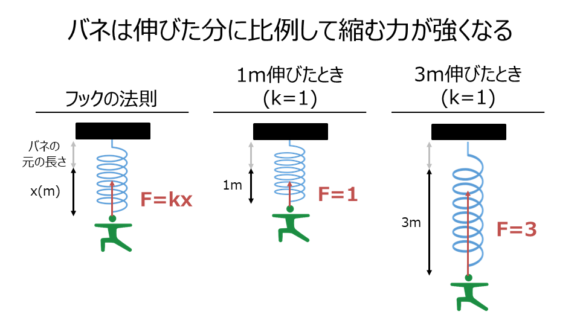
フックの法則の意味合いを具体例で考えるために、単純化してk=1とすれば、
・1mバネが伸びたら、F=kx=1・1=1。つまりバネは1の力で縮もうとする
・3mバネが伸びたら、F=1・3=3。つまりバネは3の力で縮もうとする
ということです。

厳密にはFとxは逆方向なので、力や伸び縮みの符号を考慮する（すなわちベクトルで考える）とF=-kxとなるのですが今回の議論では単純化するため符号は無視します。

バネを複数個連結させる

次にこのバネをいくつか直列に連結させてみましょう。
まずはバネ定数kのバネが2つ連結したらどうなるか考えてみます。
1つならF=kxとxだけ伸びたらkxの力で縮むバネを使います。
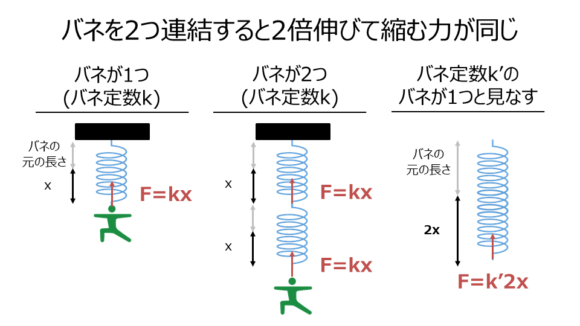
以下の図のようにこのバネを2つ繋げると、それぞれのバネがxだけ伸びてようやくF(=kx)の力を発揮することになるとわかると思います。
ここで大切なことはこのFは足し算されたりはしないということです。
バネのどの部分であっても力Fという弾性力で縮んでいるという理解が正しいです。
そして全体としてはx+x=2xだけ伸びていることになります。

つまりこの時、2つ連結したバネを全体で1つのバネと見なしてそのバネ定数をk’とまとめて置くとすれば、

$$F=kx=k’2x$$

という関係が得られ、ここから

$$k=k’2$$
$$k’=\frac{k}{2}$$

となります。
これを解釈するなら、2つ連結したことによってバネ定数が半分になったと見なせるということです。
そして、バネ定数が半分になったということは、同じだけの力を発揮するには2倍伸びないといけないし、逆に言えば同じ分だけしか伸びなければ半分の力でしか縮まないということです。
これは直感には合致しますよね。
ざっくり捉えるなら、バネが長くなれば長くなるほど伸び縮みに対して柔らかくなる、びよーんとクッション性が増す、みたいなイメージです。

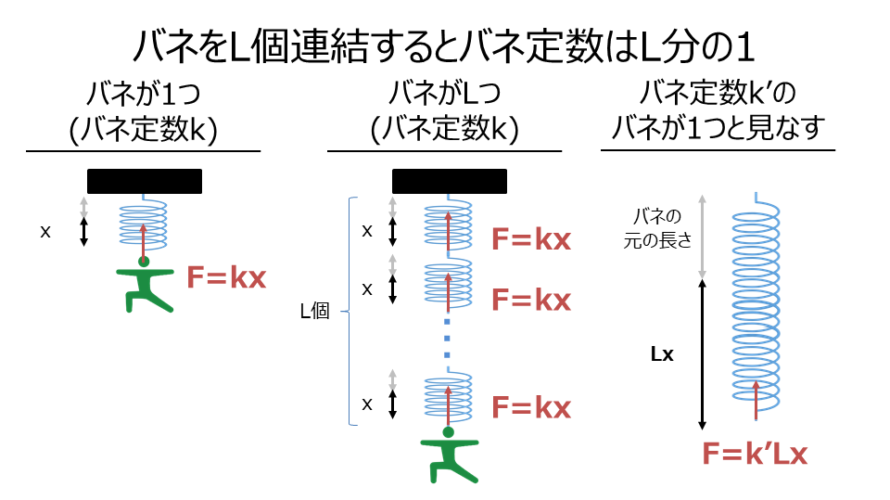
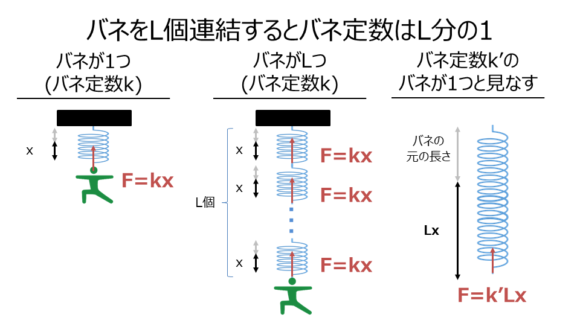
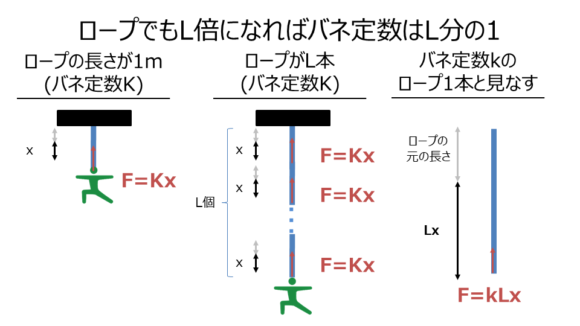
これをそのままL個の連結にまで拡張して考えます。
バネをL個連結したならば同じだけの力Fを発揮するためにはバネ1つ1つがxだけ伸びないといけない、つなわち全体としてはLxだけ伸びる必要があります。
よって式を立てると、

$$F=kx=k’Lx$$
$$k’=\frac{k}{L}$$

となり、L個連結したバネをバネ定数k’の1つのバネとしたならk’はkのL分の1になるということです。
先ほどのイメージを用いるなら、ものすごーく柔らかいバネになっていて、同じ力Fを出すにはL倍伸びないとダメだという感覚を持ってもらえるかと思います。

ロープに当てはめる

前編でロープは伸びているときは理想的にバネと見なせるという前提を置いたので、ここまでの議論はそのままロープに当てはめて良いです。
更に上ではLを自然数と考えましたが、1.5個のバネなどを想定しても全く同じ思考実験ができるのでLを有理数や実数の範囲で考えても差し支えないこともわかると思います。

すなわち、（大文字と小文字で少しわかりづらいですが）
・ロープの長さが1(m)の時のロープのバネ定数をK
・ロープがL(m)の時のバネを定数k
とするならば、

$$k=\frac{K}{L}$$

となるのです。
（今後の議論のために、先ほどkと置いていたものがK、k’と置いていたものがkになっているので比べると混乱するかもしれませんが新たに置きなおしてください）

ちなみにKはロープの長さが1(m)のときのバネ定数と置いているので、ロープの材質等のみによって決まる固有の値となります。
またkの単位は力を長さで割った(N/m)なので、KはそれにLを掛けているので単位こそ(N)すなわち力を表すのですが、このKがウェクスラーの公式に登場するロープ係数Kの正体と思ってもらえれば良いです。

要点をまとめると、以下になります。
・ロープも長くなれば長くなるほどバネの弾性的な性質から柔らかくなって、同じ力で縮むためにはより長く伸ばす必要が出てくる
・そのバネ定数kはロープの長さLに反比例する。ロープの長さ1mの時のバネ定数をKとして、k=K/Lとなる
　
　
　　

エネルギー保存則

必要なもう1つの武器であるエネルギー保存則を説明します。
本来なら運動方程式から導出するなどしてしてしっかり説明したいところですが、それは大変なのでここでは感覚的な説明に留めます。

まずエネルギーとはざっくりと「物体を動かしたり、熱を生み出したり、光を強めたりする能力」と理解して良いです。
ここでは深入りしないので日常的に使う「エネルギー」という言葉とリンクしてイメージしてもらっても全く構いません。

エネルギーは上で挙げたように様々な形態をとりますが、どのように変化してもその総量は常に保存します。
これをエネルギー保存則と呼びます。

前編でも触れましたが、この一連の議論では摩擦などがない理想的な実験を考えるのでエネルギーは初等力学的な形態のみをとるとします。
要は、熱になったり、音になったり、モノの変形に使われたりはしないということです。

具体的にロープによる墜落を想定すると、登場するエネルギーは
・重力のポテンシャルエネルギー
・ロープの弾性エネルギー
・クライマーの運動エネルギー
の3つです。

以下、1つ1つ簡単にですが説明します。

重力のポテンシャルエネルギー

地球上では質量を持つ物体は地球の重力によって地面側に引っ張られます。
物体の質量をM（kg：キログラム）とすると重力加速度g（m/s^2)を使ってその重力はMgと表すことができます。

上で述べたようにエネルギーとは「ある物体を動かす能力」と捉えられるわけですが、正確には「ある物体に仕事を与えうる能力」です。
仕事とは僕らが日常で使っている意味とは少し違い、ここでは「仕事＝力×距離」で表されます。
つまりある一定の力Fが距離Hだけ加わり続けると、F×Hの仕事がなされたと考えるわけです。

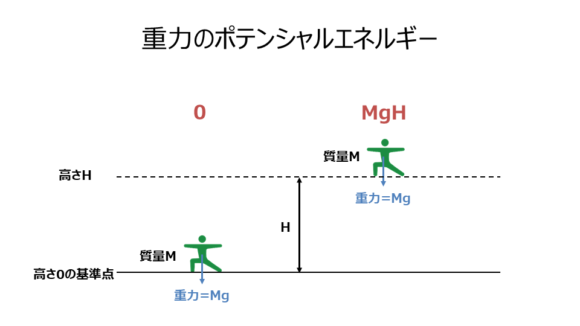
質量Mの物体には常に地球からの重力Mgがかかるので、その物体がある基準点よりもHだけ高い位置ある時、基準点の位置まで重力で落ちたらMg×Hの仕事をなされる潜在的な可能性があります。

つまり、

$$ 重力のポテンシャルエネルギー＝MgH $$

を持っていると考えることができるのです。
（正確にはその物体Mが持っているわけではなく、”場”に溜まっている、もしくは地球と物体の”力学系”に溜まっていると捉えるべきですが、物体Mが持っているとしてもここでは差し支えないです）

これが重力のポテンシャルエネルギーの意味であり、高いところにあればあるほどエネルギーが高い状態にあると見なせる理由ですね。
一般に重力の位置エネルギーなどとも呼びます。

バネの弾性エネルギー

次にバネの弾性エネルギーです。
バネが伸びたり縮んだりしていればそれだけで先端についている物体に力を与えながら移動させることができます。
つまりバネが自然の長さから伸び縮みしている状態はエネルギーを持っているということなのです。
ただ、バネの場合その伸び縮み分xに従って常に力もkxと変化するので重力の時のように単純に仕事=力×距離とはできず、積分をする必要があります。
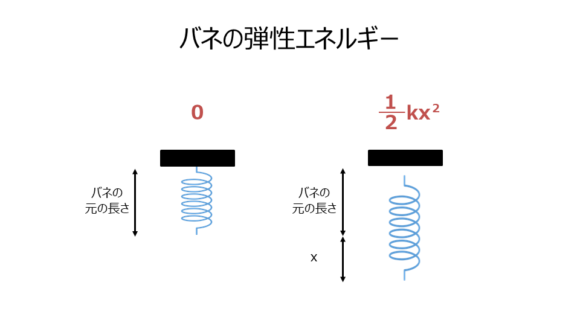
ですがここでは踏み入らずに、

$$ バネの弾性エネルギー＝\frac{1}{2}kx^2 $$

を与えられたものとして使って良いです。
バネは伸びれば伸びるほどその分量xにしたがって2乗でぐーっとエネルギーが溜まるのだな、くらいの理解でもOKです。

運動エネルギー

物体に仕事がなされると、すなわちある力で位置の変化が起きると物体は速さを持つ可能性があります。
その時動いている物体は運動エネルギーを持っている状態なのです。
物体の質量をM、速さをv、とすると運動エネルギーは

$$ 運動エネルギー＝\frac{1}{2}Mv^2 $$

と記述できるのですが、ここではこちらも所与として良いですし実は後編には登場しません。

なぜならば、この記事で考えるクライマーの状態は
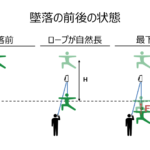
・墜落前：一番高いところにいて、ロープの伸びは無し。速さは0
・墜落後：一番低いところにいて、ロープは最も伸びている状態。衝撃荷重Fがかかっている。速さは0
の2つなわけですが、どちらもクライマーは速さ0、つまり運動エネルギーは0なのです。

後編では上の2状態でどちらも力学的エネルギーが保存する、つまり両者でエネルギーの総量は等しいという式を立ててそちらを解いていきます。 　

2次方程式の解の公式

最後はに数学の準備として2次方程式の解の公式に触れます。
ここまでで既にボリュームたっぷりなので、簡単な説明にしておきます。

方程式とは

まず方程式とは何なのでしょうか。
方程式とは「未知の数がある特定の値を取るときに成り立つ式」だと思ってください。

例えば僕の姉の年齢が未知だとしてそれをx歳としましょう。
ここで
・自分の年齢が32歳であること
・姉と自分が2歳差であること
がわかっているとします。
すると、

$$姉の年齢-2＝自分の年齢 $$
$$x-2＝32 $$

という未知数xに関して方程式を立てることができるわけです。
これをxに関して解く、つまりx=～の形にすると、
$$x=34 $$

が得られ、姉の年齢xが34歳だとわかります。

2次方程式をどう解くか

xに関する1次方程式の場合（xの2乗や3乗やそれ以上が入ってこない場合）は、簡単に解いてx=～の形にすることができます。
またxの2乗が登場するような場合でも、xの2乗の項しかない

$$x^2=4 $$

みたいな単純な形であれば

$$x＝±2 $$

というように簡単に解くことができます。

難しいのは、

$$ x^2-x-3=0$$

のような場合です。
後編でエネルギー保存則を立てるとこのようにxに関して2次の項と1次の項が入り混じった方程式が立ってしまいます。

これを解決するのが2次方程式の解の公式です。
本来僕は「公式はこうです！」とやるのが嫌なので、解の公式も導きたいのですがかなり話が逸れるのでここでは公式を所与のものとさせてください。
（そんなに導出は難しくないので、興味のある方はこちらなど）

a,b,cを実数定数（a≠0）として、xに関する2次方程式

$$ ax^2+bx+c=0$$

が成り立つ場合、xは以下の解を持つ。

$$ x=\frac{-b±\sqrt{b^2-4ac}}{2a}$$

これで準備は整いました。
いよいよ最後となる後編で、
・エネルギー保存則等の方程式を立てる
・衝撃荷重Fに関して上記の方程式を解く
・それが落下係数H/Lに依存することを確認し、その直感的な意味を考える
をやっていきましょう！

それではまた次回。
お楽しみに。

＜後編＞