クライミングの衝撃荷重はなぜ落下係数で決まるのかを初等力学で考える　前編

2019.09.18
エトセトラ上達方法数学科学するクライミング

久々の初等力学シリーズ。
今回は「ロープを使ったクライミングで落下した場合、その衝撃荷重はなぜ落下距離などではなく落下係数(クライマーが自由落下した高度差/繰り出されたロープの長さ)で決まるのか」を初等力学を使って導きます。

これまでの科学するクライミングシリーズの中でも特に初等力学シリーズは完全に僕の趣味に走り数式を前振りもなくガシガシ使っていて、おそらく大半のクライマー読者を置いてけぼりにしていた感があったはずです。
ですので今回は少し丁寧に導入から書いてみたいと思います。

この前編で
・ざっくりイメージ
・前提の確認
・注意点
などを説明し、まずは何を示したいのかを確認するとともにイメージを持ってもらいます。

そして中編では式の導出に必要な物理・数学の準備（フックの法則、エネルギー保存則、解の公式）をし、後編で実際に導出をする予定です。

1. ざっくりイメージ
2. 前提の確認
3. 衝撃荷重の解釈に関する注意点
- 3.1. 衝撃荷重は同じでも受ける撃力やエネルギーは違う
- 3.2. 落下係数は同じでもクライマーの落下スピードは違う
4. 参考文献

ざっくりイメージ

言葉の定義も交えて、この記事でどんなことを示したいのかイメージを持ってもらうために少し説明します。

落下係数、衝撃荷重、とは

まず「衝撃荷重は落下係数で決まる」と書きましたが、衝撃荷重と落下係数の定義から入りましょう。

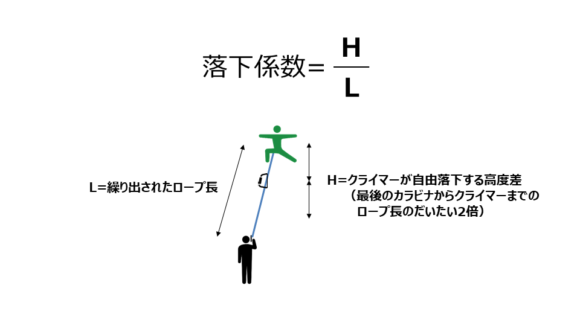
ビレイヤーとクライマーの間に繰り出されたロープの長さをL(m：メートル)、クライマーが落ちた時に自由落下する高度差をH(m：メートル)とします。
すると落下係数は

$$落下係数=\frac {H}{L}$$

で定義されます。
自由落下する高度差Hとはクライマーが落下してからロープにテンションが入り始めるまでにどのくらい落ちたかということです。
いくつかの本やウェブの情報ではHを「墜落距離」や「墜落の高度差」と書いていますが厳密にはそれは間違っていて、「自由落下の高度差」が正しいです。
クライマーが落下してロープが自然の長さに達した時点でテンションが入ることになりそこからロープが伸びてその分だけさらにクライマーは落ちますが、その伸び分はHには含まないということです。
なのでロープにたるみがなくかつ完全に直上している理想的なシンプルなルートであった場合、Hは「最後のプロテクション（ロープが止まる点）からクライマーまでのロープの長さ」の2倍になりますね。

衝撃荷重F(N：ニュートン)はクライマーがロープから受ける最大の力と定義します。
これは中編で解説しますが、クライマーが墜落してロープが最も伸び切った地点で受ける力となります。
ちなみにFの単位であるN：ニュートンは、kg・m/s^2（キログラム×メートルを秒で2回ったもの）となるのですがここは気にしないで「力の単位がニュートンなんだな」と理解してもらえれば良いです。

衝撃荷重は落下係数で決まるとは

この記事で証明したいことは「衝撃荷重FはLでもHでもなく、落下係数H/Lで決まる」ということです。
つまりどれだけロープが繰り出されたとか、どれだけクライマーが自由落下したとかには依存せず、その比率で決定するのです。
これって結構感覚と違いませんか？
なんとなくイメージすると、たくさん落下すればするほど衝撃力って大きくなりそうですよね？
しかしそうではないということを示すのがこの記事の目的です。

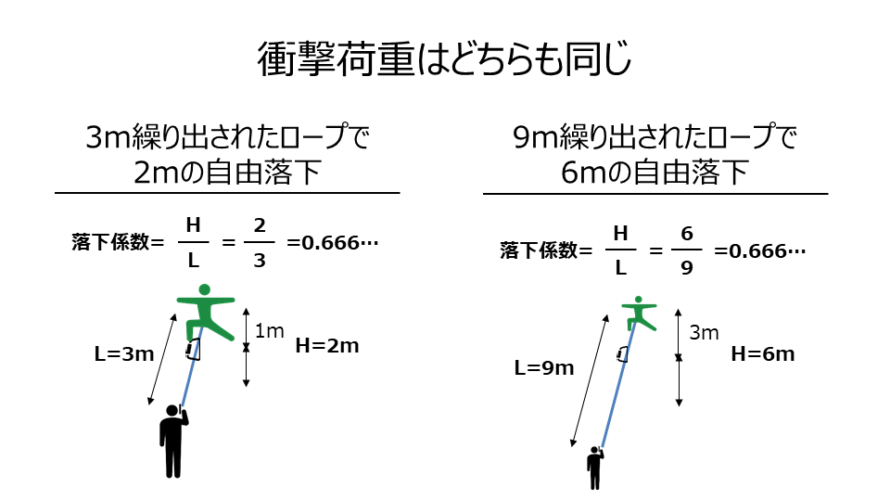
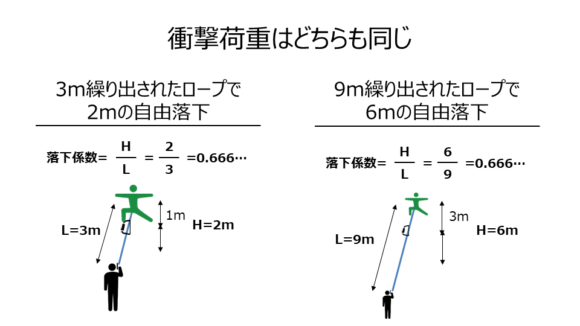
具体例で考えます。
・3mのロープを繰り出していて（L=3）、自由落下する高度差が2m（H=2。理想的な直上ルートなら、最後のカラビナからクライマーまで距離が1m）
・9mのロープを繰り出していて（L=9）、自由落下する高度差が6m（H=6。理想的な直上ルートなら、最後のカラビナからクライマーまで距離が3m）
の場合は、自由落下の距離に3倍もの違いがあるにも関わらずどちらも

$$落下係数=\frac {H}{L} =\frac {2}{3}= \frac {6}{9} =0.666… $$

となり、落下係数は同じ、つまり衝撃荷重Fも同じということなのです。

ウェクスラーの公式

衝撃荷重Fを数式で表すと以下のようになります。

$$F=Mg+Mg\sqrt{1+2\frac{H}{L}\frac{K}{Mg}}$$

M(kg：キログラム)はクライマーの質量
g(m/s^2：メートルを秒で2回割る）は重力加速度
というのですが、Mgでクライマーが受ける重力となるのでこれらはまとめて捉えて良いです。
K(N：ニュートン)はロープ係数などと呼ばれるのロープ固有の値なのですが、単位はNであることから力を表します。
中編で説明しますがロープの弾性力とざっくり思っておいてください。

注目すべき点は上の式を見るとわかるように、MgもKもロープとクライマーが同じならシチュエーションに依らず常に一定。つまりFを左右するのは落下係数H/Lのみであるということです。

この式はウェクスラーの公式と呼ばれています。
そしてこのブログの目的は
・ウェクスラーの公式を導出する
・なぜFは落下係数H\Lで決まるのか、ウェクスラーの公式をできる限り直感的に理解する
ということになるわけですね。

前提の確認

これでざっくりイメージとこの記事の目的は共有できました。
ただ実は上の話は色々な前提を元に、結構話をシンプルにしているのでその前提を確認しておきます。
厳密さが気にならない人はここは読み飛ばしてもOKです。

ロープは理想的なバネの特性を持つ

式の導出にあたり、ロープは（伸びている時のみ）線形的な弾性力を持つという前提を置きます。
つまり理想的なバネであると見なすということです。
中編で説明しますが、要はフックの法則に従い伸びれば伸びるほどその伸び分に比例して戻ろうとする力を発揮するということですね。
ロープの物性に僕はそれほど詳しくないですが現実的には例えばすごくロープが伸び切ってしまった時とかはバネ的な挙動を示さないということもあるかなと思います。
しかしそうではなくて、常に伸びた分だけ力は強くなるよという前提を置かせてもらいます。

ロープ係数Kは常に一定だとする

ロープの弾性力を現すロープ係数Kは「いつでも」「どこでも」一定という前提も置きます。
これも現実ではきっとロープの箇所とか、伸び具合によってKは変わってくるはずなのですがそういうことは起こらないで理想的に常に一定としましょうということです。

カラビナ等の摩擦は無視

設定をシンプルにするために、プロテクションのカラビナなどから受ける摩擦などは0であるとします。
理想的に落下したクライマーの力が全てロープにかかるものとします。

スタティックビレイをおこなう

これは結構重要なのですがクライマーをロープで確保しているビレイヤーはスタティックビレイ（固定確保）をするという前提を置きます。
つまりクライマーが落下した瞬間にロープの長さは完全に固定されそれ以上全く繰り出さないし、ビレイヤーも動かないということです。

実はウェクスラーの公式にはダイナミックビレイをおこなった際の衝撃力Fを算出するバージョンもあるのですが、そちらは後編で少しだけ触れます。

衝撃荷重の解釈に関する注意点

前編の最後に衝撃荷重の解釈の注意点を書いておきます。
本来なら全て論じた後に書こうかと思ったのですが勘違いする人もいるかと思うので先に断っておきます。
まず衝撃荷重Fは落下係数H/Lに依存すると書きましたが、現実世界では落下係数が同じであってもHが大きければ大きいほど一般的に危険は高まります。
なぜかはざっくり以下の2点で説明できます。

衝撃荷重は同じでも受ける撃力やエネルギーは違う

後編で少し触れますが、落下係数が同じで衝撃荷重Fも同じであってもクライマーが長く落下すればクライマーがFを受ける時間の長さや距離が長くなります。
するとクライマーやカラビナがロープから受ける撃力（＝力積変化）や仕事（＝エネルギー変化）と呼ばれるものが大きくなるのです。
人体やカラビナへのダメージや破損には衝撃荷重Fだけでなくその足し合わせである、受けた撃力やなされた仕事も大きく影響するはずです。
込み入った物理の話に入るのをここでは避けますが、衝撃荷重Fが同じだからダメージも変わらない、というのはおそらく誤りだと思います。
参考文献にいくつかそのあたりの話も出ているので興味のある方は調べてみてください。

落下係数は同じでもクライマーの落下スピードは違う

落下係数H/Lでロープから受ける衝撃荷重Fは決まりますが、クライマーの落下のスピードは異なります。
先の例ではHが2mと6mで落下係数が同じでしたが、当たり前ですが6m自由落下したときの方がクライマーの落下スピードは速いです。
理想的に何にも当たらずにロープにだけ「びよーん」と墜落すればロープから受ける衝撃荷重Fは同じかもしれませんが、現実世界では落下の途中で岩などにぶつかる可能性があります。
すると当然ですが速いスピードで岩に当たった方が人体が岩から受ける衝撃荷重、撃力、エネルギーは大きいので怪我のリスクも高まります。
なのでロープから受ける衝撃荷重Fが同じであるということがすなわちリスクが同じであることには全くならないということがわかるかと思います。

　
　
前提確認や注意点が長くなりましたが、前編はここまでです。
次は中編で、衝撃荷重Fの導出に必要な物理や数学の基礎を少し丁寧に説明していきたいと思います。
お楽しみに。

＜中編＞

クライミングの衝撃荷重はなぜ落下係数で決まるのかを初等力学で考える　中編

＜後編＞

クライミングの衝撃荷重はなぜ落下係数で決まるのかを初等力学で考える　後編

参考文献

この記事を書くにあたっての参考文献などを紹介します。
僕もまだ読み切っていない、理解しきっていない本やウェブサイトが多いですが。

・常吉の酔いどれ日記：ロープの衝撃荷重の算出法
このブログは素晴らしいです。
物理的な考察も間違いがないし、クライミングへの理解も深い。
はっきりいってこの常吉の酔いどれ日記さんのエントリーを僕は少し丁寧に解説しているに過ぎないので、上に貼った記事が理解できれば僕がこれから書くことは読まなくてもOKなくらい。
このエントリー以外にも読みごたえがある内容が多いです。

・特殊高所技術の広場(ロープ高所作業,ロープアクセス）：ナイロンスリングで直接セルフビレイを取ると危険です。　ナイロンスリングでの短距離落下試験
「酔いどれ～」さんからリンクで飛びましたが、実際に落下実験などをしている素晴らしい記事。
まだ僕もしっかり読み込めていないですが、実際にデータを取っているのがすごいです。

・Yutaka Miura’s home page：落下係数
落下係数や衝撃荷重に関して算出する方法の参考になります。このページからリンクが貼られているものも読むとためになるはず。

・ALTERIA：落下率と衝撃荷重 (理論）
落下係数と衝撃荷重についてビジュアルを元にわかりやすく説明されています。
アルテリア（PETZL）のこの教科書的なシリーズは他のものも超参考になるので必読。

・雪崩知らずの山スキー：衝撃荷重
衝撃荷重に対して筆者が勘違いしていたところから説明してくれているので読みやすいです。

・『大人の山岳部』
ウェクスラーの公式が載っています。他にも参考になることが書いているので持っていて良い本です。