クライミングの衝撃荷重はなぜ落下係数で決まるのかを初等力学で考える　後編

ロープを使ったクライミングで落下した場合、衝撃荷重はなぜ落下距離などではなく落下係数で決まるのかを初等力学で考える、の後編。
ここまで前編と中編で、
・落下係数や衝撃荷重などの言葉の定義や説明
・衝撃荷重が落下係数で決定するという意味
・必要となる物理や数学の導入
を書いてきました。

この後編ではいよいよ衝撃荷重Fを求め、そして導かれた式の意味を確認してみましょう。

＜前編＞

＜中編＞

墜落前と墜落後の状態

目的は衝撃荷重F(N)を求めることです。
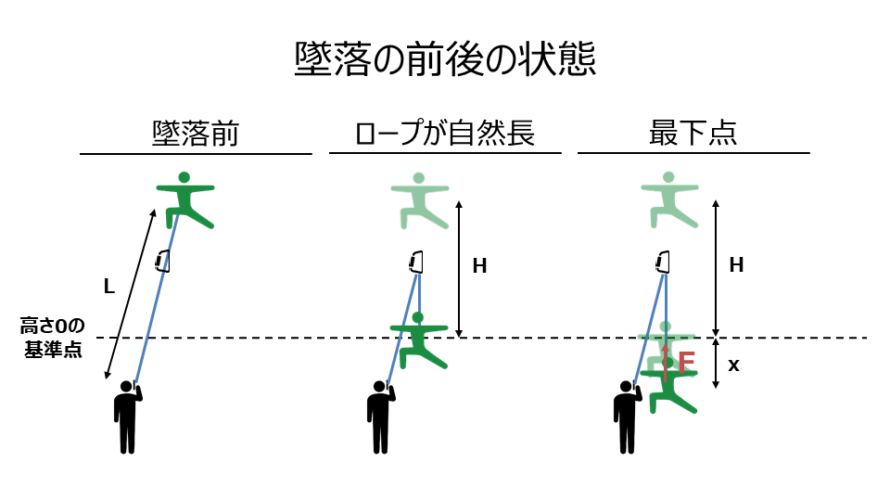
もう一度墜落の前後の状態を確認しましょう。
高さはどこを基準としても良いのですが、墜落してロープが自然長となった瞬間（つまりロープにテンションが入る瞬間）を高さ0mの基準点とします。

・墜落前
　繰り出されたロープの長さ：L(m)
　高さ：H(m)
・最下点（衝撃荷重Fがかかる）
　繰り出されたロープの長さ：xだけロープが伸びているので、L+x
　高さ：xの分だけ落ちているので-x

最下点でロープは最大限に伸びているので、最大の力となる衝撃荷重Fがクライマーにかかっています。

フックの法則とエネルギー保存則を立てる

ではいよいよ衝撃荷重Fを求めましょう。

フックの法則

中編で取り上げたように繰り出されたロープの長さがLのときのバネ定数をkとすると、フックの法則から

$$F=kx$$

kはロープの長さLに依存する値であり、こちらも中編で見たようにロープ係数（ロープの長さが1mの時のバネ定数）K(N)を用いて

$$k=\frac{K}{L}$$

と表せます。すなわち、

$$F=\frac{K}{L}x・・・①$$

ロープ係数Kはロープに固有の値、またLは墜落前の状況によって決まっているので、上の式において未知の数は衝撃荷重Fとロープの伸び分xとなります。

エネルギー保存則

未知の数が2つ、式が1本、では一般的に方程式は解けないのでもう1本式を立てます。
それがエネルギー保存則です。

墜落前と最下点でそれぞれ力学的エネルギーを全て書き出しそれらが等しい、という式を立てます。
中編で触れたように力学的エネルギーはこの場合、
・重力のポテンシャルエネルギー
・ロープの弾性エネルギー
・クライマーの運動エネルギー
の3つのみを考えればよいのですが、墜落前も最下点もどちらもクライマーは速さを持たない止まっている状態なので運動エネルギーは考えなくて良いです。

墜落前

墜落前はロープの長さはLであり、自然長からの伸び分は無いです。
つまりクライマーはロープから引っ張る力は受けないので、ロープの弾性エネルギーは0。
すなわち重力によるポテンシャルエネルギーのみを考えれば良いので、クライマーの質量をM、重力加速度をgとすると、

$$墜落前のエネルギー=MgH$$

となります。
クライマーがHという高さにいることで、全体としてはMgHというエネルギーを保有しているということです。

最下点

衝撃荷重Fがかかる最下点では、ロープがxだけ伸びているので弾性エネルギーが生じます。
また高さも基準点からxだけ低いところにいるので、重力のポテンシャルエネルギーはマイナスとなります。
これらより、

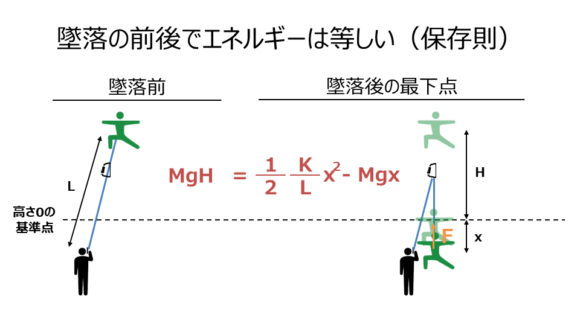
$$最下点のエネルギー=\frac{1}{2}kx^2-Mgx= \frac{1}{2}\frac{K}{L}x^2-Mgx $$

という式が立ち、エネルギー保存則から、

$$墜落前のエネルギー=最下点のエネルギー$$

$$MgH= \frac{1}{2}\frac{K}{L}x^2-Mgx ・・・②$$

となります。
この式はロープの伸び分x以外は全て既知の数であるので、xに関する2次方程式です。
よって中編で扱った2次方程式の解の公式からxを求めることができるのです。

ロープの伸び分xを求める

式②をxに関して整理すると、以下になります。

$$\frac{1}{2}\frac{K}{L}x^2-Mgx-MgH=0$$

2次方程式の解の公式

$$ ax^2+bx+c=0$$

$$ x=\frac{-b±\sqrt{b^2-4ac}}{2a}$$

に当てはめるために以下と置きます。

$$a=\frac{1}{2}\frac{K}{L}$$

$$b=-Mg$$

$$c=-MgH$$

よってロープの伸び分xは

$$ x=\frac{ Mg ±\sqrt{ {(Mg)} ^2+4 \frac{1}{2}\frac{K}{L} MgH }}{2 \frac{1}{2}\frac{K}{L} }$$

$$= \frac{L}{K} \left( Mg ±Mg\sqrt{ 1+2\frac{H}{L}\frac{K}{Mg}}\right) $$

となります。
落下係数H/Lが登場しているので、わかりやすくまとめました。

±があるので計算上xは2つの解を持つのですが、ルートの中身は1以上であるため±がマイナスの場合xは負の値を取ります。
今xは「ロープが自然長から落下方向へ伸びた分」と置いているので、xが負ということは自然長の位置よりもロープが縮んでいるケースなので想定している場合には適しません。
よってxが正である、以下がロープの伸び分となります。

$$x= \frac{L}{K} \left( Mg +Mg\sqrt{ 1+2\frac{H}{L}\frac{K}{Mg}}\right)・・・③ $$

（踏み込んで考えたい人への説明。
ロープは自然長よりも縮んだ場合、つまりxが負の場合、は弾性エネルギーを持ちません。
しかしなぜxが負の場合も解となりえるかというと、ここではエネルギー保存則をロープがあたかもバネであるかのように弾性エネルギーを持つとして立てたからです。
つまりクライマーがロープが自然長の基準点となる高さよりも上にいる範囲内にも、バネの弾性エネルギーと重力のポテンシャルエネルギーが丁度元の全エネルギーと一致する地点があるのです。）

衝撃荷重Fを求める

衝撃荷重Fは③を①へ代入することで求められ、

$$F=\frac{K}{L} \frac{L}{K} \left( Mg +Mg\sqrt{ 1+2\frac{H}{L}\frac{K}{Mg}}\right) $$

$$= Mg +Mg\sqrt{ 1+2\frac{H}{L}\frac{K}{Mg}}・・・④$$

となります。
これはまさに前編で書いたウェクスラーの公式に他なりません。

これでめでたく衝撃荷重Fを既知の数値で表すことに成功しました。

結果の解釈

さてここから式④を色々と解釈していきましょう。

衝撃荷重Fは落下係数H/Lで決定する

④を見るとわかるのですが、
・Mg：クライマーにかかる重力でありクライマーで決定
・K：ロープ係数であり使用するロープで決定
するので、落下係数H/L以外はクライマーの高度、繰り出されたロープの長さ、プロテクションの位置、などによらず常に一定です。
つまり衝撃荷重Fはやはり落下係数H/Lで決定するのです。

ロープの伸び分xは落下係数H/Lで決定しないが、、、

一方でロープの伸び分xは式③を見るとその先頭にLが掛かっていることから、落下係数H/Lでは決定しないです。

$$x= \frac{L}{K} \left( Mg +Mg\sqrt{ 1+2\frac{H}{L}\frac{K}{Mg}}\right)・・・③ $$

なので前編の一番最初に想定した落下係数が0.666…の2つのシチュエーション
ⅰ 3mのロープを繰り出していて（L=3）、自由落下する高度差が2m
ⅱ 9mのロープを繰り出していて（L=9）、自由落下する高度差が6m
ではロープの伸び分xはⅱの方が3倍大きいです。

これは感覚と一致しますね。
“スケールが3倍なのだから、落ちた時にロープも3倍伸びるでしょう”と。
しかしここでロープの弾性力を表す式①に立ち返ると

$$F=\frac{K}{L}x・・・①$$

となっていて、分母にLがあることがわかります。
要はロープを繰り出した伸びた分だけバネ定数が低下する、イメージとしてはバネが柔らかくなっているのです。
なので衝撃荷重Fを求める際に、式③のロープの伸び分xにかかるLとこの式①（フックの法則）の分母のLが互いに相殺し、Fは落下係数にのみ依存するという形になっていることがわかります。

まとめると、以下のように理解できるでしょうか。
・ロープの伸び分xはロープの繰り出しLに応じて大きくなる
・ロープの繰り出しLが大きくなると、バネ定数k(＝K/L)は小さくなる。ロープのバネとしての性質が柔らかくなるイメージ
・衝撃荷重Fはkxで求まるのでFにとってはLの項は相殺し、系全体の比率を決める落下係数H/Lのみが項として残る

結局はウェクスラーの公式がなぜこの形になるのかはエネルギー保存則を解かないといけませんが、Lの項がなぜ消えるかなどは感覚として掴むことは可能かと思います。

その他の項の意味合いなど

ウェクスラーの公式④の他の項の意味合いも見ておきましょう。

$$F= Mg +Mg\sqrt{ 1+2\frac{H}{L}\frac{K}{Mg}}・・・④$$

クライマーの重力Mg

Mgが増えれば衝撃荷重Fは増える形になっていますし、Mgが0ならFももちろん0です。
これは重いクライマーほど衝撃荷重が大きく、体重0なら衝撃は0という感覚と一致します。

ロープ係数K

ロープ係数Kが大きいというのはロープがものすごい硬いというイメージで良いです。
するとKが大きければ大きいほど衝撃荷重Fが大きくなるというのは納得できますね。
逆にKが0だともはやバネ的な性質が完全になくなってどこまでも伸びてしまうロープになるのですが、一応③からxが無限大に発散するのでこれも結果としては納得です。

落下係数H/Lが最小値0の場合

物理において極端な場合を考えて結果を解釈することは大切です。
落下係数H/Lが最小値となる0の場合を考えてみましょう。
これは自由落下の距離Hがないということなので、真っすぐ垂れているロープにぶら下がったという状況に等しいですね。
④から

$$F= Mg +Mg\sqrt{ 1+0}=2Mg$$

が導かれます。
すなわち、ロープに自由落下なしにびよーんとぶら下がっただけでも体重の2倍の力がクライマーにかかるということです。
一見これは直感に反します。
しかしロープを理想的なバネと見なしているのでこの結果は正しいのです。
バネはその最下点で逆向きに引き戻す力が強く働きます。
その力がクライマーの体重の2倍だというわけです。
ただし現実的には摩擦などへエネルギーは逃げますし、ロープは伸びる方向にしかバネ的な挙動は示さないので、その振動はすぐに落ち着きクライマーへの重力Mgとバネからの弾性力が釣り合って安定な状態となります。

落下係数H/Lが最大値2の場合

落下係数の最大値はプロテクションを取らずに落下した場合であり、その時H=2Lつまり落下係数は2になります。

④から

$$F= Mg +Mg\sqrt{ 1+2・2\frac{K}{Mg}}= Mg +Mg\sqrt{ 1+\frac{4K}{Mg}} ・・・④$$

となります。
当然ですが、この衝撃荷重がクライマーへの重力Mgの何倍になるかは完全にロープ係数Kによって決定します。
使うロープの規格を調べればこの式から最大の衝撃荷重が計算できるというわけです。

終わりに＆残された論点

3記事に渡ってお付き合いいただいてありがとうございました。
結局のところは式を追わないと完全には理解しきれない部分がありますが、少しはロープの物理学が身近に感じていただけたなら幸いです。

残された論点としては、以下2点でしょうか。

ウェクスラーの公式が実際にどの程度現実世界と当てはまるのか

ロープ係数Kが一定を保てなくなる、フックの法則が正しく働かなくなる、エネルギーの散逸が起きる、などによって衝撃荷重Fがウェクスラー公式からどのくらい離れるのかがデータなど取れたら面白いですね。
前編に載せた参考文献にこのような実験結果がおそらくあったかと思いますがまだ読み込めていないです。

ダイナミックビレイ時のウェクスラーの公式の導出

実際のビレイはダイナミックビレイ、つまり墜落してから停止するまでにロープをある程度繰り出します。
その繰り出し分をS(m)と置くと、ウェクスラーの公式は以下のように書けるといくつかの文献に書いてあります。

$$F= Mg -K\frac{S}{L}+Mg\sqrt{ 1+2\frac{H}{L}\frac{K}{Mg}+ \left(\frac{S}{L}\frac{K}{Mg}\right)^2 }・・・④$$

しかしちょっと手を動かしたところこの導出が上手くできないです、、、。
もしご存じの方、導出できた方いたら教えてもらえるとありがたいです。

　

では長くなりましたがこんなところで終わりにします。
また次回もよろしくお願いします。