1度しか試行できない確率的な物事とどう向き合うべきか

この間書いた「1秒の価格のパラドックス」にいろいろな意見をもらえて嬉しかったので、もう1つ数学とか心理学とか行動経済学っぽい話で昔からふと考えているけれどわからないことを書いてみる。
生活の中で確率や期待値を意識したり、目にすることは多い。
・降水確率40%
・サイコロは1/6の確率で1の目が出る
・300円の宝くじの期待値は143円
などなど。
これらは正しく扱えば非常に役に立つ情報である。
降水確率40%の日に岩場に行くことを1,000回チャレンジしたなら、400回くらいは雨に降られてしまうけれど600回くらいはクライミングできるだろう。
サイコロを何百回も振れば、1の目は6回に1回に近い頻度で出るだろう。
300円の宝くじをどんなにたくさん買っても、多くの人はそれに払ったお金の半分以下しか返ってこないだろう。
一方で人生においては上記のようにたくさんはトライできない「何度も試行できない物事」というものもある。
例えば、大学受験。
模試などからあなたの第一志望校の国立校の合否判定が20%と算出されたとしよう。
(この確率の妥当性は受け入れ、同等の学力の生徒の5人に1人が合格することは統計的に正しいとする)
どうしても現役で国立に行きたい場合、あなたは20%に賭けて迷いなく第一志望を受けるだろうかそれとも志望校を下げるだろうか。
受験なら実際の場合は私立併願もあるし、浪人の選択肢もあるし、なにより努力で20%の数字を向上させることも可能だ。
また落ちても死ぬわけじゃないから、人生全体から見たらここは大した問題ではなくそれこそ悔いが無いように好きにすれば良いのかもしれない。
では本当に生死にかかわるくらい重大な物事の場合はどうだろうか。
僕は学生時代の最後にネパールのカトマンズ・ルクラ間の飛行機に、妻(当時は彼女)と乗ったことがある。
ルクラは山の斜面に位置するため、これはかなり危険なフライトとして有名だ。
僕らは当時その路線が墜落したことがあるという情報は知っていたが、特段迷うことなく飛行機を利用してエベレスト街道のトレッキングを楽しんだ。
しかし僕らが乗った2009年を挟むようにして、2008年、2010年、2011年、2012年とほぼ毎年のように墜落事故が起きている。
この墜落確率がどの程度か適当な前提でざっと考えてみると
・2年に1度墜落事故が起きる(さすがに5年中4年は当たり年が続いたのだろう)
・1日20便飛行機が飛ぶ(実際は天候で飛ばない日もあるし、20便なのかは知らない)
として、
365(日)×20(便)×2(年)=14,600
つまり約15,000分の1の確率で死ぬかもしれない賭けに僕らは出たことになる。
さて、この確率を高いと見れば良いのか、低いと見れば良いのか。
そして今後もこのような万が一死ぬかもしれないチョイスを迫られた時はどのように判断すればよいのか。
この記事で考えたい事
前置きが長くなったが、この記事で考えたい事は以下である。
・人生において個人として1度もしくは少ない回数しか試行できない物事をやるかやらないかの判断は僕らはどう下せば良いのか
・その判断に確率、期待値、分散、などは役に立つのか。役立つならどう役立てれば良いのか
・特に生死に関わるなど失敗できない重大な決断の場合この判断基準をどう持てば良いのか
少し僕がこれまでに考えたこと、今思っていることを書いてみる。

少ない試行回数においては確率や期待値は意味がないのか
上記の問いに対してパッと思いつくのは「期待値を判断に使用する」という答えである。
既に例として挙げた宝くじなら
・各等賞が当たる確率
・各等賞で貰える賞金
を全て掛け合わせると、約143円となるが、それがすなわち期待値だ。
この期待値をもってして「143円より高いお金で宝くじを買うことは損だ」と言う人がいるし、僕もそう考えることが多い。
しかし忘れてはならないのは期待値というのはあくまで「十分多い回数試行した時にリターンがそこに収斂する」という意味しかもたない。
なので1本だけ買って1億円が当たるかもしれないし、当然何も当たらないかもしれない。
とにかく宝くじ全てを買ったら1本あたりの賞金が約143円になるというだけなのだ。
何が言いたいのかというと、1度もしくは少ない回数しか試行できない物事に期待値を持ち出すことはあまり意味をなさないのではないかと思う。
大学で僕は理系の研究室に入っていたが、全く他分野の就職を決めた時に教授が「専門外だし、クビもあるし、期待値を考えたら理系職に就いた方が良いぞ」と言ってきたことがある。
これに対して「1度しか試行できない新卒就職というものに期待値を考える意味があるのでしょうか?」と答えたことを覚えている。
確率や期待値が関係ないからといって無謀な賭けに出ていいのか
しかし1度しか試行できないからと言って、無謀すぎる賭けに出て良いのだろうか。
あえて色々な例で考えてみる。
統計的に女性が普通に妊娠する確率は年齢と共に低下する。
1年間で自然妊娠する確率は45~50歳だと5%程度だというデータもある。(詳しい出所や、計算の分母と分子が何なのかなどは不明だが)
もし僕が年齢と妊娠確率の関係を多数回試行できる立場、例えば厚生労働大臣か何かで日本全体の出生率や妊娠数を向上させたい立場など、ならば「女性が若くして妊娠しても不自由なく生活できる政策」のようなことを打ち出すかもしれない。
対して、これがイチ個人の話であれば人生は1度しか訪れないので、20歳でも妊娠できないかもしれないし、50歳でも妊娠できるかもしれない。
少ない試行回数では確率や期待値は正確な意味をなさないのだから、これはそれぞれの個人の人生ではどうなるかはわからない。
とは言えあなたが「自分の人生ではどうしても子供が欲しい!」と考えるのならやはり若くして妊娠することを試みた方が良いだろう。
しかし、もし同時に「なんだけれど、若い内はバリバリ働きたいからできるだけ遅い年齢で子供が欲しい」と考えたとしたら、一体何歳で妊娠を狙うということに妥協点を見いだせば良いのだろうか。
このような非常に重大な人生のテーマの確率と効用をみんなどのように判断しているのだろうか。
リスクヘッジできるもの、できないもの
一連の疑問に答えを与えようとするならば「リスクヘッジできるものはする」である。
ある危険なことが起きることを予期して、そのリスクに予め対応できるように構えることを、リスクヘッジするという。
保険などは典型的なリスクヘッジだ。
例えば車の運転という「小さい確率だが相手や自分に大損害を与える可能性のある」とんでもない乗り物になぜ僕らは乗れるのかといったら、車の保険に入ることで万が一のケースをリスクヘッジできているからである。
保険は入ることそれ自体は期待値としては損である。
つまり加入者を全員平均したら払った額よりも貰った額の方が少なくなる。
しかしなぜみんな保険に入るのかと言えば、万が一の最悪のケースをリスクヘッジできるからに他ならない。
つまり先ほど書いた3つ目の「 生死に関わるなど失敗できない重大な決断」ならば、事前にリスクヘッジできるものはしておく、というのが人生でゲームオーバーにならない一つの考えなのかもしれない。
超高価な家など買うなら地震保険とか火災保険に入った方が良いし、金融商品になけなしの財産を投資するとしても色々なケースを想定してポートフォリオを組んでリスクヘッジした方が良い。
ただ全てのことがリスクヘッジできるわけではない。
ネパールのカトマンズからルクラへ行く場合は飛行機に乗らず何日もかけてバスと歩きを使うということが可能だが、墜落する可能性のある飛行機にどうしても乗らなければ目的地に行けないがどうするかという判断に迫られることがあるかもしれない。
その場合、死ぬ可能性があるのだから保険をかけたところで自分の死に対してリスクヘッジは本質的にはできない。
なので結局僕らは、その飛行機が墜落する確率がいくつ以上なら乗るべきではないのか、飛行機で目的地に着くことが自分にどの程度の効用をもたらすのか、などを考えて決断をしないといけない。
そしてその決断の基準はどうなるのか、という当初の問いに戻ってしまう。
みんな一体どうやって判断して決断しているのか。
僕はもう一度ルクラに行きたかったら飛行機に乗るべきなのか乗らないべきなのか。
果たしてこの問いに納得がいく答えはあるのだろうか。
参考になる記事と脱線
最後に参考までに2つほど。
佐山展生さんの言葉
こういう話に対して
「結局、上手くいくかいかないかの2つに1つ!確率1/2ですよ!」
などと結論付けるのは詭弁でありあまり好きじゃない。
一方で、この記事の趣旨とは少しずれるが、佐山展生さんがnews picksの記事で発言していた
「 成功確率5%に挑戦すると、人生はエキサイティングになる」
というのは面白い。
帝人から銀行に転職をしたときも、95%くらいの確率で失敗すると思っていたがチャレンジを取ったそうだ。
これは確率的な物事に対してどう判断を下すのかということにおいて人生を通して指針となる言葉だ。
サンクトペテルブルクのパラドックス
せっかくなので少し脱線した期待値の話。
あなたは以下のゲームに1回あたりいくら払うだろうか。
「表と裏がそれぞれ1/2の同確率で出るコインがある。
裏が出続ける限りはコイントスを続けられて、表が出たら終了。
「コイントスできた回数」だけ1円を倍にした金額が貰える。
例えば、
裏表なら、1円×2=2円
裏裏裏裏裏表なら、1円×2×2×2×2×2=32円
貰うことができる。」
人によるが、何となく10円くらいなら払っても良いかなという感覚だろうか。
数学ができる人なら「期待値を計算して、期待値以下の金額なら払った方が得だ!」と言うかもしれない。
では、期待値を考えてみよう。
1円が貰えるのはいきなり表の時なので、1/2の確率
2円が貰えるのは、裏表、なので1/2×1/2=1/4の確率
4円が貰えるのは、裏裏表、なので1/2×1/2×1/2=1/8の確率
8円が貰えるのは、裏裏裏表、なので1/2×1/2×1/2×1/2=1/16の確率
・・・
2のn乗円が貰えるのは、裏がn回のあと表のときなので、(1/2)のn+1乗の確率
ここから期待値を計算、すなわち貰える金額と確率を掛け合わせると
期待値=1/2+1/2+1/2+1/2+・・・・+1/2+・・・
と1/2を足すことが永遠に続き、期待値は発散して∞となる。
よって期待値でこの賭けに払える金額を決めるならば「いくら支払っても良い」となってしまうのだ。
これをサンクトペテルブルクのパラドックスと言う。
詳しくはwikipediaでも読んでみて欲しいが、期待値が日常的な感覚と乖離する良い例となっている。
お気づきだと思うが無限回試行できることを前提に期待値が算出されていることがパラドックスの要因となっているのだ。
期待値を判断に安易に使うことは危険を伴うこともある。
最後はだいぶ話がそれました。
うまく僕の疑問やもやもやが伝わったでしょうか。
ではまた明日!
-
前の記事
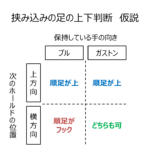
クライミングの挟み込み、右足で踏むか?左足で踏むか? 2019.02.20
-
次の記事

名前が決まっていないクライミングのホールディングやムーブ 2019.02.21
