ボルダリングのグレードの足し算

ボルダリングの課題を作っていると、2つの課題の繋げモノ的な場合にグレーディングに迷うことがあります。
例を挙げると、2級の課題をやった後にまた短い2級的なムーブが入る様な課題をグレーディングする場合です。
課題を通してのマックスの強度が2級に収まっているから2級とするのか。
それとも前半の2級よりも明らかに悪いのだから1級や初段にすべきなのか。

以前ブログで触れた、
ボルダリングのグレードの決定方法～前編：グレードの定義、前提となる考え～
ボルダリングのグレードの決定方法～後編：難易度の構成要素～
などの自分の考えに従えば、元の2級よりも持久力という要素が加味されたために登れるクライマーの数は減るはずなのでグレードを上げるべきとなりますが、どの程度のグレードアップをすれば良いかまではわかりません。

そんなことを考える内に、こういったグレードの足し算に関する面白い記事を以前にネットで目にしたことを思い出したのでそちらを紹介しつつ、色々と考えてみたいと思います。

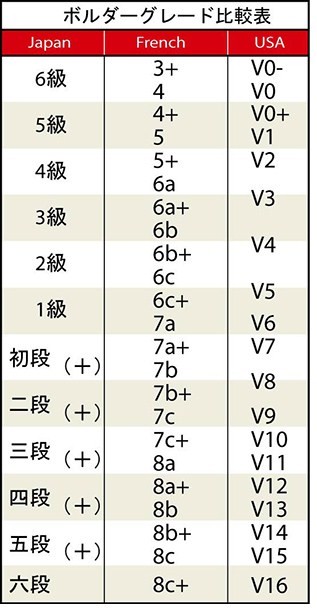
予備知識：段級グレードとVグレードの換算

まず今回の主題に入る前に、日本でなじみのある段級グレードとアメリカを中心に使われているVグレードの一般的な換算表を載せておきますね。

CLIMBING-netより転載

また、これはあくまで換算表の1つの考え方であり、感じ方は人それぞれです。
例えば小山田さんの場合また少し違った換算をしています。

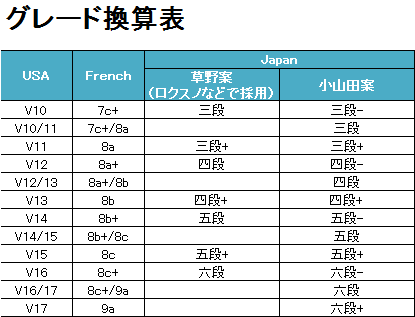
まぁすっごいラフに考えると
・V10が三段
・Vグレード2つ分で一段分
みたいに考えておけば外さないです。
（そういや以前こんな記事も書きました：ボルダリングのグレード換算の公式）

Australian Bouldering.comによるグレードの足し算

前置きが長くなりましたが、いよいよ本題。
冒頭に書いた面白い記事とはAustralian Bouldering.comに載っていた、「Elementary grading: 1 + 1 = 3」なのですが、そこではオーストラリアのVグレードに関して以下の足し算が当てはまると主張しています。

Vn + Vn-3 = Vn
Vn + Vn-2 = Vn+1
Vn + Vn-1 = Vn+1
Vn + Vn = Vn+2

（nは3以上の整数）

例を挙げてみるとイメージが掴めるかもしれません。

V7 + V7 =V9
馴染のある段級グレードに換算すると、
初段 + 初段 = 二段+。

V7 + V4 = V7
初段 + 2/3級 = 初段のまま。

つまりざっくり言うと、
同じグレードを2つ繋げると1段（or級）くらい上がる
1.5～2段（or級）以上離れているグレードの課題を繋げてもグレードは上がらない
とAustralian Bouldering.comは主張しているのです。

おそらくいくつかの既存課題からこの公式を揚げているのだと思いますが、これはその正確性や汎用性があるのかは検証する余地があるものの、斬新な考え方で非常に面白いと思います。

日本の岩の課題で考えてみる

ではさっそくこの式が日本の岩の課題に当てはまるのかを考えてみます。

・「那由多」（六段- V16）　※わかりやすく小山田さんの換算グレードで考えます
まずはこの四月に小山田大さんが初登した「那由多」（六段- V16）。
「那由多」は下呂にある課題ですが、「涅槃那」（五段　V14/15）と「プレセム」（五段- V14）リンクした課題です。
（実際に那由多の詳細を知らないので、厳密にこの2つの課題を繋げているわけでなかったらすみません）

上にあげた式から
V14/15 + V14 =V16
となるので、まさにぴたりと当てはまっています！

SNSなどでは
“五段と五段を繋げて六段にしかならないのか”
的な声もちらほら見られましたが、Australian Bouldering.comの主張は小山田さんの体感とそうズレてはいないようです。

・「蟹虫」（四段 V12）
次は日本で一番有名な繋げモノかもしれない御岳の「蟹虫」（四段 V12）。
「蟹虫」は「蟹」（三段 V10）と「虫」（三段 V10）を繋げた課題です。
厳密には、「蟹」パートに関しては核心とも言える飛ばしの一手が無く、虫も初手が省略されるので完全に繋げているとは言えませんが。
こちらもなんと
V10 + V10 =V12
とまさに公式通りなのです！

・「忘却の河」（二段 V8/9）
最後に少し悩ましい例として小川山の「忘却の河」（二段 V8/9）を挙げます。
こちらは「グレード不明の前半部分」（V？）に「マントル」（2級 V4/5)を足したものです。
前半部分はグレーディングされていませんが、逆に考えればあの式を使えば前半部分のグレードが推定できるのではと考えるわけです。

V？ + V4/5 =V8/9

これを解くと、なんとV？=V8/9となります！笑
つまり「忘却の河」は前半部分からおにぎりっぽいガバあたりまでいった時点で既に二段程度あるということになってしまいます。

補足

ここまで読んでお気づきの方もいるとは思いますが、式が現実と整合しない点をいくつか指摘します。

1つ目は最後に挙げた「忘却の河」のように、
既存課題に一部のムーブを足すことで前の課題から2グレード以上上がっている場合、足されたムーブの部分だけで全体課題と同じグレードである、となってしまう点です。
他の例を挙げれば例えば神戸の「フルチャージ」（四段 V12）。
「フルチャージ」の後半部分は「電池切れ」（二段 V8/9）ですが、この式で考えると前半部分だけでV12が付くことになってしまいます。
これは明らかに現実とそぐわないですね。

2つ目は決定的におかしい点なのですが、実はこの式は結合法則が成り立たないため、計算をどこから始めるかで結果が変わってしまいます。笑

例えばV4の課題にV1を4個繋げる課題があったとしましょう。
まず前から順に足したとします。
=V4 + V1 + V1 + V1 + V1
どれだけV4にV1を足してもグレードはV4のままなので
=V4
となります。

しかし先に後半のV1のところを足してみると
=V4 + (V1 + V1) + (V1 + V1)
=V4 + V3 + V3
=V4 + V5
=V6

となるのです！
つまりこの式、実は全然厳密じゃないです！笑

最後に

今回の記事は散々検証しておいて最後に落とすスタイルですみません。
まぁあくまでちょっとしたお遊びの式ですね。
そもそもどのようなタイプの課題を繋げるかで全くグレーディングは変わるはずなので一概に数字だけで足し算できるはずはないですし。
しかしそれでもAustralian Bouldering.comのようにグレードの足し算に関する主張はそれほど目にしたことがなかったので個人的にはとても面白いなと感じました。
厳密性はないものの、ある程度のグレーディングの指針にはなり得るかもしれません。

みなさんも時間があれば既存課題を例にいくつかこの式を当てはめてみると面白いかも。

ではでは。